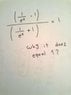- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Why does the limit of [(1/e^x)-1] / [(1/e^x)+1] equal -1 as x goes to infinity?
- Thread starter YYaaSSeeRR
- Start date
-
- Tags
- Limit
In summary: And the answer is not -1. It is 1. In summary, the limit of [(1/e^x)-1] / [(1/e^x)+1] as x approaches positive or negative infinity is 1, not -1. This can be seen by multiplying the numerator and denominator by e^x, which simplifies the expression to (1-e^x)/(1+e^x). As x approaches infinity, 1/e^x approaches 0, making the fraction approach -1/1 = -1. However, as x approaches negative infinity, 1/e^x also approaches 0, making the fraction approach 1/1 = 1. Therefore, the limit is 1, not
Physics news on Phys.org
- #2
Infrared
Science Advisor
Gold Member
- 1,084
- 658
Are you sure the answer is 1? The limit should be -1.
- #3
YYaaSSeeRR
- 53
- 0
sorry I forgot to put the - , yea it does equal -1 but why?
- #4
Infrared
Science Advisor
Gold Member
- 1,084
- 658
What is [tex] \lim_{x\rightarrow \infty} {e^{-x}-1}?[/tex]
[tex]\lim_{x\rightarrow \infty} {e^{-x}+1} ?[/tex] Just divide these two answers.
[tex]\lim_{x\rightarrow \infty} {e^{-x}+1} ?[/tex] Just divide these two answers.
- #5
- 22,183
- 3,325
HS-Scientist said:What is [tex] \lim_{x\rightarrow \pm\infty} {e^{-x}-1}?[/tex]
[tex]\lim_{x\rightarrow \pm\infty} {e^{-x}+1} ?[/tex] Just divide these two answers.
That only works for the limit to ##+\infty##.
- #6
YYaaSSeeRR
- 53
- 0
micromass said:That only works for the limit to ##+\infty##.
yes and that drives me crazy
- #7
Infrared
Science Advisor
Gold Member
- 1,084
- 658
micromass said:That only works for the limit to ##+\infty##.
Thanks, fixed.
For negative x, multiply the numerator and denominator by [itex] e^x [/itex]
- #8
YYaaSSeeRR
- 53
- 0
so what about when x→-∞ ?
- #9
- 22,183
- 3,325
YYaaSSeeRR said:so what about when x→-∞ ?
First things first. Do you understand the limit when ##x\rightarrow +\infty##?
- #10
YYaaSSeeRR
- 53
- 0
micromass said:First things first. Do you understand the limit when ##x\rightarrow +\infty##?
yes I do.
- #11
- 22,183
- 3,325
YYaaSSeeRR said:yes I do.
Cool. For the other limit, you'll need to follow the hint in #7.
The answer won't be -1, by the way.
- #12
YYaaSSeeRR
- 53
- 0
For negative x, multiply the numerator and denominator by ex
I have not seen this after the modification :)
thanks a lot ,this problem forced me to throw the book away.
- #13
- 22,183
- 3,325
YYaaSSeeRR said:I have not seen this after the modification :)
thanks a lot ,this problem forced me to throw the book away.
So you found the right answer??
Also: you might want to post this in "calculus and beyond" next time
- #14
YYaaSSeeRR
- 53
- 0
micromass said:So you found the right answer??
Also: you might want to post this in "calculus and beyond" next time
yes I got the right answer.
you must see teachers here in Syria ,they drive you crazy.
can't wait till I graduate high school and arrive to the US.
- #15
YYaaSSeeRR
- 53
- 0
actually when I followed hint #7 the answer wasn't -1 ,so Micromass what is the right answer?
- #16
ChaseRLewis
- 43
- 0
(e^-x - 1) / (e^-x +1)
Multiply num and denom by e^x
(1 - e^x) / (1 + e^x)
so you if you got positive 1 with negative infinite that makes sense as that reduces to
1/1 = 1
Multiply num and denom by e^x
(1 - e^x) / (1 + e^x)
so you if you got positive 1 with negative infinite that makes sense as that reduces to
1/1 = 1
- #17
YYaaSSeeRR
- 53
- 0
ChaseRLewis said:(e^-x - 1) / (e^-x +1)
Multiply num and denom by e^x
(1 - e^x) / (1 + e^x)
so you if you got positive 1 with negative infinite that makes sense as that reduces to
1/1 = 1
(1 - e^x) / (1 + e^x) when x→-∞
yea it does equal 1 , but in my textbook when x→-∞ the equation (e^-x - 1) / (e^-x +1) equal -1 and that make no sense for me.
- #18
- 22,183
- 3,325
If your textbook says the answer is -1, then your textbook is wrong. The answer is 1.
- #19
HallsofIvy
Science Advisor
Homework Helper
- 42,988
- 981
Are we still talking about "[(1/e^x)-1] / [(1/e^x)+1]" as x goes to infinity? For very large x, 1/e^x is very close to 0 so the fraction is close to -1/1= -1.
(Oh, I see. The original post said "as [itex]x \to \pm\infty[/itex]" and the limit as x goes to negative infinity is 1.)
(Oh, I see. The original post said "as [itex]x \to \pm\infty[/itex]" and the limit as x goes to negative infinity is 1.)
- #20
- 22,183
- 3,325
HallsofIvy said:Are we still talking about "[(1/e^x)-1] / [(1/e^x)+1]" as x goes to infinity? For very large x, 1/e^x is very close to 0 so the fraction is close to -1/1= -1.
No, we're talking about the limit to ##-\infty##.
FAQ: Why does the limit of [(1/e^x)-1] / [(1/e^x)+1] equal -1 as x goes to infinity?
Why does this limit equal 1?
The limit in question is likely a specific mathematical expression that approaches a value of 1 as the input approaches a certain value. This means that as the input gets closer and closer to that value, the output gets closer and closer to 1. This is known as a limit and can be calculated using calculus.
What does a limit of 1 mean?
A limit of 1 means that the output of a mathematical expression approaches a value of 1 as the input approaches a certain value. This can be interpreted as the expression getting closer and closer to 1 without ever actually reaching it.
How is a limit of 1 calculated?
A limit of 1 can be calculated using calculus, specifically the concept of limits and derivatives. This involves using mathematical rules and techniques to find the behavior of a function as the input approaches a certain value. The limit is then the value that the output approaches as the input gets closer to that value.
Can a limit equal 1 for all values of the input?
No, a limit of 1 is a specific value that the output approaches as the input approaches a certain value. It does not necessarily mean that the output will always be 1 for all inputs. There may be other values of the input for which the output is different.
Why is it important to understand limits that equal 1?
Limits that equal 1 are important in calculus because they help us understand the behavior of functions and their outputs as the inputs approach certain values. This is useful in many real-world applications, such as predicting the behavior of a system or optimizing a process. Understanding limits also helps to build a foundation for more advanced mathematical concepts.
Similar threads
- Replies
- 2
- Views
- 1K
- Replies
- 7
- Views
- 860
- Replies
- 5
- Views
- 1K
- Replies
- 7
- Views
- 2K
- Replies
- 7
- Views
- 1K
- Replies
- 8
- Views
- 1K
- Replies
- 14
- Views
- 2K
- Replies
- 12
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 5
- Views
- 2K
Share: