I Why Does the Negative Sign Appear in the Vector Potential Equation?

[deuteron]

TL;DR Summary

.

We have motivated the derivation of the vector potential in the following way:

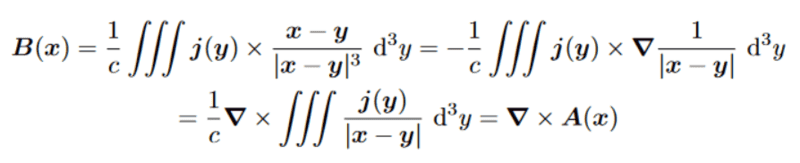
However, I cannot understand where the $-$ sign in the second equality came from. I thought that it was because the gradient was with respect to the $y$-variable, and then using the product rule one could explain the transition to the last expression, but in that case $\nabla_{\vec y}\times\vec j(\vec y)$ would have to be zero, which I am not really sure is necessarily true; and in that case I would again not understand how a $\nabla_{\vec y}$ would become a $\nabla_{\vec x}$, since at $\nabla\times \vec A(\vec x)$ I assume $\nabla$ must be acting on the $\vec x$
That's why I don't see how the left and right hand sides of the third, fourth, and possibly the fifts $=$ signs are equal to each other, can someone please help me?

 

[kuruman]

You know that
$\nabla_x \dfrac{1}{|x-y|}=-\dfrac{x-y}{|x-y|^3}=-\nabla_y \dfrac{1}{|x-y|}$
It follows that
$\dfrac{x-y}{|x-y|^3}=+\nabla_y \dfrac{1}{|x-y|}=-\nabla_x \dfrac{1}{|x-y|}.$

So the second equality is $$=-\frac{1}{c}\int \int \int j(y)\times\nabla_x \dfrac{1}{|x-y|}d^3y$$Does this help?

 

[deuteron]

but in that case how do we take $\nabla_{\vec x}$ out of the integral? It wasn't cross multiplied with $\frac 1 {|\vec x-\vec y|}$, but now it is?

 

[kuruman]

The vector identity says
$\vec{\nabla}\times(\psi~\vec A)= \psi \vec{\nabla}\times\vec A+\vec{\nabla}\psi\times \vec A.$
Here you identify
$\vec{\nabla}\rightarrow \vec{\nabla}_x$
$\psi \rightarrow \dfrac{1}{|x-y|}$
$\vec A \rightarrow \vec j (y)$

What do you get when you put these in the identity?