Why Does $\vec{n}.\vec{r}$ Equal $d$ for a Parallel Line?

[ognik]

I must have a mental block here!
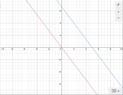
Given r(t) = (x(t), y(t)) = (-3t, 4t) - clearly this passes through the origin.

Eliminating t results in $4x + 3y = 0 $. Normalising gives $\frac{4}{5}x + \frac{3}{5}y = 0 $ which we can write as $ \vec{n}.\vec{r}=0 $ , i.e. $ \vec{n} = \left(\frac{4}{5}, \frac{3}{5}\right) $. Cool.

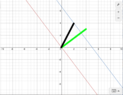
Now we look at a line parallel to r(t), a distance d from the origin in the direction of $\vec{n}$. Clearly the normal to this line is also $ \vec{n} = \left(\frac{4}{5}, \frac{3}{5}\right) $

My book now says $ \vec{n}.\vec{r}=d $! But I think $ \vec{n}\: \& \: \vec{r}$ are also orthogonal, so shouldn't $ \vec{n}.\vec{r}$ always $=0 $?

(The example goes on to have this new, parallel line pass through (3, 0), then the eqtn for this line is 4x + 3y = 12 (which I am happy with) , then they use $ \vec{n}.\vec{r}=d $ to find $ d = \frac{12}{5} ...$)

 

[GJA]

Hi ognik,

I think looking at the attached picture should help. The position vector $$\vec{r}$$ for the red line will always be perpendicular to $$\vec{n},$$ but by shifting the line away from the origin, the position vector $$\hat{r}$$ for the blue line is not always perpendicular to $$\vec{n}.$$ Given that $$\hat{r}$$ is to be a displacement of $$\vec{r}$$ by a distance of $$d$$ in the direction of $$\vec{n},$$ can you see a way to write the equation for $$\hat{r}$$ that will give $$\vec{n}\cdot\hat{r}=d$$?View attachment 4914

 

[ognik]

Hi and thanks GJA, but I still don't get why the blue line might not be perpendicular to $\vec{n}$- it is parallel to the red line, therefore at the same angle to all lines through the red line - like the normal = $\frac{\pi}{2}$ ?

Reversing this perspective, if not perpendicular, then the lines are not parallel, in which case $\vec{n}$ would not be the normal to the blue line...

 

[GJA]

Hey again ognik. I think what's possibly being overlooked is that a position vector is always drawn from the origin.

In the case of the red line, the position vector for each point on the line is some scalar multiple of $$(-3,4);$$ i.e. $$\vec{r}=(-3,4)t$$.

However, in the case of the blue line, the position vector for each point on the line (drawn from the origin) is not always perpendicular to $$\vec{n}.$$ This is because the points on the blue line are not all described as a scalar multiple of $$\vec{r}.$$ Specifically, the position vector for the blue line is the original vector $$\vec{r} $$ shifted by $d$ units in the direction of $$\vec{n}.$$ It is this shift, combined with the fact that position vectors are drawn from the origin, which makes the position vector for the blue line not perpendicular to $$\vec{n}$$ for every point on the shifted (blue) line.

For example, in the attached image, the green vector $$5\vec{n}=(4,3)$$ is not perpendicular to the black position vector for the blue line. This implies that $$\vec{n}$$ is not perpendicular to the position vector either.

Let me know if this picture helps clear up the confusion.View attachment 4917

 

[ognik]

Thanks GJA, I am really trying to get my head around this; I know you & the book are right, I just want to understand why...maybe there is some subtlety of notation or convention I don't appreciate ...with that thought:

I am 100% that the position vector for $\vec{blue}$, will not always be $\perp$ to \vec{n}; in fact I think it will never be - it is only the blue vector itself that is always perpendicular to the original $\vec{n}$. For shortest d, the position vector for a point on the blue vector will be co-linear with $\vec{n}$.

But what is $\vec{r}$? I thought it was the red line, because $\vec{n}$ must be perpendicular to $\vec{r}$ for the original condition of $\vec{r}.\vec{n} = 0$. Are you saying that $\vec{r}$ for the blue line is now the position vector for $\vec{blue}$? In which case I would need to understand why $\vec{r}$ for the red line is not just the zero vector - with no direction?

 

[I like Serena]

My book now says $ \vec{n}.\vec{r}=d $! But I think $ \vec{n}\: \& \: \vec{r}$ are also orthogonal, so shouldn't $ \vec{n}.\vec{r}$ always $=0 $?

Hi ognik,

A vector along the line is always orthogonal to $\vec n$.
However, $\vec r$ is not along the line. Instead it's a vector from the origin to the line.

Now suppose $\vec r_0$ is some vector on the line.
Then the vector along the line is $\vec r - \vec r_0$ which must be orthogonal to $\vec n$.
So:
$$(\vec r - \vec r_0) \cdot \vec n = 0
\quad\Rightarrow\quad \vec r \cdot \vec n = \vec r_0 \cdot \vec n = d$$

Furthermore, since $d$ is the dot product of a point on the line with the unit normal, $d$ is the distance of the line to the origin.

 

[ognik]

Thanks guys, that's all clear now, just misunderstood what r was