annamal
- 393
- 33
- TL;DR Summary
- Why doesn't the released mass m2 on pulley have higher acceleration since it is no longer subject to the upward force of tension?
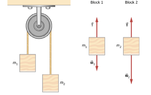
Consider the pulley in the attached image to be frictionless. (a) If m2 is released, what will its acceleration be?
My question is why wouldn't m2's acceleration be greater if released rather than attached to the string because m2 released is no longer subject to the string's upward force tension?
My question is why wouldn't m2's acceleration be greater if released rather than attached to the string because m2 released is no longer subject to the string's upward force tension?