Why f is no longer a function of x and y ?

[Adesh]

TL;DR Summary

When we restrict the domain a function then why it is no longer a function of $x$ and $y$?

Good Morning!

If I have function of two variables $f(x,y)$ and if we write it like this $$ z = f(x,y)$$ then it means that for every point in the $xy$ plane there is a point above/below it and is related to it by $f$. In simple words, every point in $xy$ plane has a point associated with it. We can say that $f$ in this case is a function of both $x ~\textrm{and}~y$, because $f$ is varying as $x ~\textrm{and}~y$ are changing, and consequently it's derivative with respect to $x$ or $y$ is not zero.

Now, if we imagine that $z=f(x,y)$ but only those $x~\textrm{and}~ y$ are allowed which lie in the defined rectangular region:

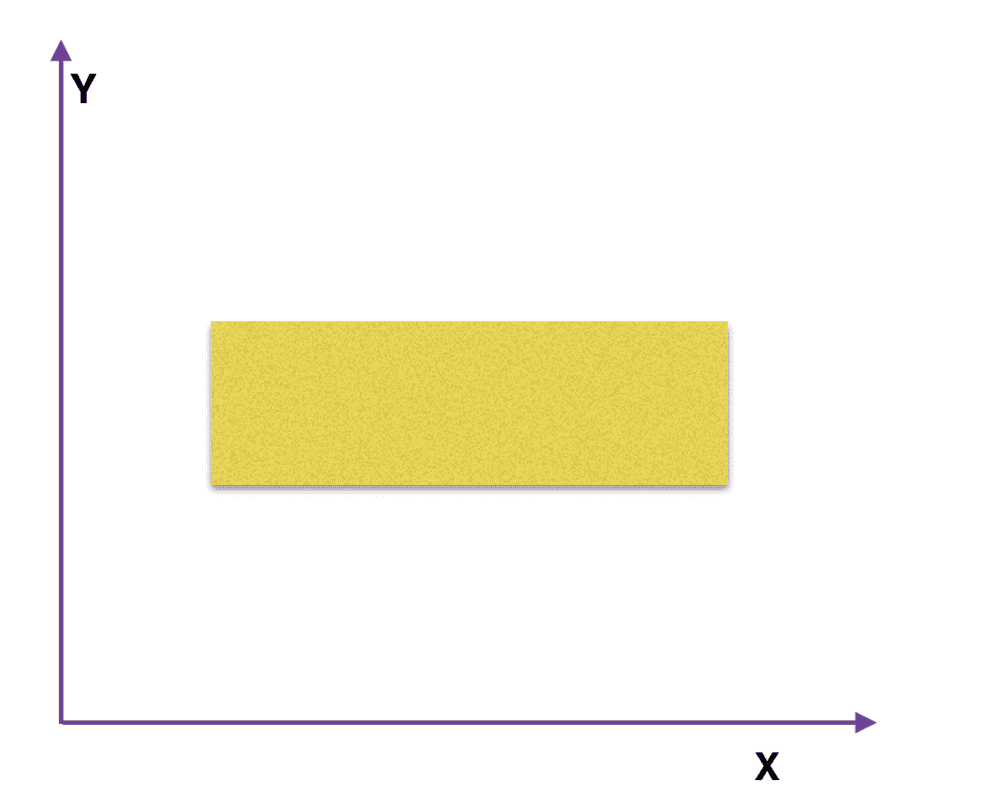
let's assume that the corners of the rectangle have coordinates: $(2,2) ; (4,2) ; (4,4) ; (2,4)$. And let's say any point lying in that rectangle is represented as $(a, b)$. So, the function now looks like this $$ z= f(a, b)$$. My problem is: why $f$ is no longer a function of $x ~\textrm{and}~y$ . After all, $a~\textrm{and}~y$ are just the different symbols, we can even write our function as $$ z = f(x,y) ~~~~~~~~~~~~\bigg\{ 2\lt x,y \lt 4 $$ So, why $f$ is no longer a function of $x$ and $y$, and why is the derivative of $f$ (I mean after the restriction is defined) is zero?

 

[mitochan]

You case seems
$$z=f(x,y)$$
where
$$2<x<4,\ 2<y<4$$
z or f you say is a function of x and y.
Partial derivatives
$$\frac{\partial f}{\partial x}|_{y=const.}$$
$$\frac{\partial f}{\partial y}|_{x=const.}$$
would be available and there is no reason that they are always zero.

 

[PeroK]

In your example $f$ is still a function of $x,y$. But with restrictions on the value of $x$ and $y$.

There's no need to change to variables $a, b$.

 

[Adesh]

Then why here Griffith has done that (I may be wrong in my actual question) :

The Biot-Savart Law for the general case of a volume current reads $$ \mathbf{B} \left(
\mathbf{r}
\right)
= \frac {
\mu_0}
{4 \pi}
\int \frac {
\mathbf{J} \left(\mathbf{r'}\right) \times \mathcal{\hat r}
}
{\mathcal{r^2}} d\tau' $$
This formula gives the magnetic field at a point $\mathbf{r}= (x, y, z)$ in terms of an integral over the current distribution $\mathbf{J} \left(x', y', z'\right)$. It is best to be absolutely explicit at this stage $$ \mathbf{B}~\textrm{is a function of (x, y, z)} \\
\mathbf{J} ~\textrm{is a function of (x', y', z')}\\
\vec{\mathcal{r}} = (x- x') \hat x + (y-y') \hat y + (z-z') \hat z \\
d\tau ' = dx'~dy'~dz'$$
The integration is over the primed coordinates; the divergence and the curl of the $\mathbf{B}$ are with respect to the unprimed coordinates. $$ \nabla \cdot \mathbf{B} = \frac{ \mu_0}{4\pi } \int \nabla \cdot \left( \mathbf{J} \times \frac{ \mathcal{\hat r} } {\mathcal{r^2} } \right) d\tau'$$

Invoking the product rule $$ \nabla \cdot \left( \mathbf{J} \times \frac {\mathcal{\hat r}}{\mathcal{r^2}}\right) = \frac{\mathcal{\hat r}}{\mathcal{r^2}} \cdot \left(\nabla \times \mathbf{J} \right) - \mathbf{J} \cdot \left( \nabla \times \frac{\mathcal{\hat r}}{\mathcal{r^2}}\right)$$

But $\nabla \times \mathbf{J} =0$ because J doesn't depend on the unprimed variables.

 

[PeroK]

I can see no relationship between posts #1 and #4. What's going on?

 

[Adesh]

My main problem is the last line, when he says "But $\nabla \times \mathbf{J}=0$ because J doesn\t depend on the unprimed variables".

Well, although $\mathbf{J}$ is variable of $x', y' , z'$ but after all it lies in the space of $x, y ,z$ only, isn't it? If we think of a slab lying in space and current is flowing through this 3D slab of conducting material, then the points inside the slab have the coordinates $x' , y' , z'$ but they lie in the $x, y, z$ space.

 

[Adesh]

I can see no relationship between posts #1 and #4. What's going on?

I was just writing post #6.

 

[PeroK]

My main problem is the last line, when he says "But $\nabla \times \mathbf{J}=0$ because J doesn\t depend on the unprimed variables".

Well, although $\mathbf{J}$ is variable of $x', y' , z'$ but after all it lies in the space of $x, y ,z$ only, isn't it? If we think of a slab lying in space and current is flowing through this 3D slab of conducting material, then the points inside the slab have the coordinates $x' , y' , z'$ but they lie in the $x, y, z$ space.

What you're missing can be shown in the following:

$f(x) = \int_0^1 xt dt$

Here $f$ is a function of $x$ and $t$ is a (dummy) integration variable. More generally, we could have:

$f(x) = \int_0^1 g(x, t) dt$

If we differentiate $f$ with respect to $x$, then we have:

$f'(x) = \int_0^1 \frac{\partial g}{\partial x} \ dt$

In your example, Griffiths is using $x', y' z'$ as the dummy integration variables. In any case, these are not the same variables as $x, y, z$ with which he is differentiating. Any function of $x', y', z'$ that does not involve $x, y, z$ at all must have zero derivative with respect to $x, y, z$.

 

[Adesh]

If we differentiate f with respect to x, then we have:
$f'(x) = \int+0^1 \frac{\partial g}{\partial x} \ dt$

I'm not able to understand this. I understood your first equation and second equation.

I'm unable to understand why $\mathbf{J}$ wouldn't not vary as we move along the $x-$axis (which is just another way of saying that J is a function of x).

 

[PeroK]

I'm not able to understand this. I understood your first equation and second equation.

I'm unable to understand why $\mathbf{J}$ wouldn't not vary as we move along the $x-$axis (which is just another way of saying that J is a function of x).

It isn't a function of $x$; it's a function of $x'$.

One issue here is what it means to take a derivative inside an integral. That's where the distinction between $x$ and $x'$ is important.

You ought to question that step.

 

[Adesh]

It isn't a function of $x$; it's a function of $x'$.

One issue here is what it means to take a derivative inside an integral. That's where the distinction between $x$ and $x'$ is important.

You ought to question that step.

If we relate this to my first post, then $x'$ is the abscissa of any point inside the yellow (defined region) rectangle, and hence x' is a function x. Am I relating two very different things?

 

[PeroK]

If we relate this to my first post, then $x'$ is the abscissa of any point inside the yellow (defined region) rectangle, and hence x' is a function x. Am I relating two very different things?

You're problem lies in not fully understanding a dummy integration variable; and the subtleties that arise when you "take the derivative inside an integral".

If we go back to my first example:

$f(x) = \int_0^1 xt dt$

Here, without anything fancy we can see that:

$f(x) = x\int_0^1 t dt = \frac x 2$

Hence $f'(x) = \frac 1 2$.

We can also get that by:

$f'(x) = \int_0^1 \frac{\partial}{\partial x}(xt) dt = \int_0^1 t dt = \frac 1 2$

But, we can't get that by doing what you want to do and treat $t$ the same as $x$:

$f'(x) = \int_0^1 \frac{\partial}{\partial x}(xt) = \int_0^1 x + t dt$

This simple example shows how wrong it is to try to differentiate $t$ as though it were $x$, when $t$ is not the variable $x$.

$t$ is replaced by $\vec J(x', y', z')$ in your example, but the same applies. If you think $x'$ looks too much like $x$, then use $u, v, w$ instead of $x', y', z'$.

 

[Adesh]

It may seem silly but why I'm thinking that $x'$ is a subset of $x$ or that $x'$ is just a portion of $x$ and hence is differentiable w.r.t $x$? . I fully understood your example and thank you for making it so clear.

 

[PeroK]

It may seem silly but why I'm thinking that $x'$ is a subset of $x$ or that $x'$ is just a portion of $x$ and hence is differentiable w.r.t $x$? . I fully understood your example and thank you for making it so clear.

$x'$ is a distinct dummy integration variable. In some cases your points $x$ may be outside some region, over which you are integrating. Sometimes $x$ is inside the region of integration. It's the term $\vec r - \vec r'$ that makes your integral depend on $\vec r$. If you didn't have that, the integral would be just a constant. But, with $\vec r - \vec r'$ inside the integral, the value of the integral becomes a function of $\vec r$.

 

[FactChecker]

Just because the primed variables and unprimed variables are in the same coordinate system does not mean that they are equal or related. So the partial derivatives can be completely different. Apparently you have a function that is not dependent on the unprimed variables at all, so those partial derivatives are zero.

 

[Adesh]

Just because the primed variables and unprimed variables are in the same coordinate system does not mean that they are equal or related. So the partial derivatives can be completely different. Apparently you have a function that is not dependent on the unprimed variables at all, so those partial derivatives are zero.

I don't know why but I'm getting this thought and reasoning again and again that primed variables are just a defined interval of unprimed variables. If you don't mind may I describe my whole reasoning to you. I think I have disturbed @PeroK sir too much and he has explained his points many times but my brain couldn't understand him but he was very patient too in explaining his things. May I describe my thinking to you?

 

[PeroK]

I don't know why but I'm getting this thought and reasoning again and again that primed variables are just a defined interval of unprimed variables. If you don't mind may I describe my whole reasoning to you. I think I have disturbed @PeroK sir too much and he has explained his points many times but my brain couldn't understand him but he was very patient too in explaining his things. May I describe my thinking to you?

Here's an idea. Let's take the Coulomb force between two charged particles of fixed charge at points $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$. The force has magnitude:
$$F(x_1, y_1, z_1, x_2, y_2, z_2) = \frac{q_1q_2}{4\pi \epsilon_0 ((x_1 - x_2)^2+ (y_1 - y_2)^2 + (z_1 - z_2)^2)}$$
$F$, therefore, is a function of six spatial variables, if you allow the two particles to be placed anywhere. That means that the function $F$ is not a function of 3D space. It's a function of two sets of 3D space.

 

[archaic]

If we relate this to my first post, then x′x′ is the abscissa of any point inside the yellow (defined region) rectangle, and hence x' is a function x. Am I relating two very different things?

Call the $x$-axis $φ$, for example. If I tell you that I will draw on $φ$ both xx and $x'$, does that mean that they are the same?
It is just a custom that we call the axis "the $x$-axis" and use a variable called $x$.
Your reasoning is true insofar as that what you mean by "$x′$ depends on $x$" is that it depends on the axis, not the variable.
The $\varphi$-axis or $x$-axis are just the set $\mathbb{R}$ here.
I hope that I haven't misunderstood you.

 

[Adesh]

Here's an idea. Let's take the Coulomb force between two charged particles of fixed charge at points $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$. The force has magnitude:
$$F(x_1, y_1, z_1, x_2, y_2, z_2) = \frac{q_1q_2}{4\pi \epsilon_0 ((x_1 - x_2)^2+ (y_1 - y_2)^2 + (z_1 - z_2)^2)}$$
$F$, therefore, is a function of six spatial variables, if you allow the two particles to be placed anywhere. That means that the function $F$ is not a function of 3D space. It's a function of two sets of 3D space.

Yes I’m getting something, just because it depends on six variables doesn’t mean that it depends on six orthogonal axes system, :) please please gradually after it.

 

[Adesh]

Call the $x$-axis $\varphi$, for example. If I tell you that I will draw on $\varphi$ both $x$ and $x'$, does that mean that they are the same?
It is just a custom that we call the axis "the $x$-axis" and use a variable called $x$.
Your reasoning is true insofar as that what you mean by "$x'$ depends on $x$" is that it depends on the axis, not the variable.
I hope that I haven't misunderstood you.

Wow! $x’$ depends on axis (which we call x-axis) but doesn’t depend on $x$, I think it’s a great explanation. Sir, please explain what does it mean to differentiate something w.r.t. to $x$. My current knowledge says that it means how much the function changes when x is changed by a differential amount dx, and then we take the ratio of change in x and change f.

 

[archaic]

Wow! $x’$ depends on axis (which we call x-axis) but doesn’t depend on $x$, I think it’s a great explanation. Sir, please explain what does it mean to differentiate something w.r.t. to $x$. My current knowledge says that it means how much the function changes when x is changed by a differential amount dx, and then we take the ratio of change in x and change f.

I have modified my answer before you post this one to further clarify what is meant by axis.

 

[PeroK]

Yes I’m getting something, just because it depends on six variables doesn’t mean that it depends on six orthogonal axes system, :) please please gradually after it.

"Orthogonal" only has meaning when you define vectors. We don't define a vector with six components here, as that isn't very useful. Instead, we look at the domain of the function $F$ as $\mathbb{R}^3 \times \mathbb{R}^3$. Rather than $\mathbb{R}^6$.

In any case, what would you do if I asked you to differentiate $F$ above with respect to $y_2$?

 

[Adesh]

I have modified my answer before you post this one to further clarify what is meant by axis.

I have understood from your post is that $x$ is any arbitrary point on $\phi$ axis and $x’$ is also an arbitrary point on $\phi$ axis.

 

[Adesh]

"Orthogonal" only has meaning when you define vectors. We don't define a vector with six components here, as that isn't very useful. Instead, we look at the domain of the function $F$ as $\mathbb{R}^3 \times \mathbb{R}^3$. Rather than $\mathbb{R}^6$.

In any case, what would you do if I asked you to differentiate $F$ above with respect to $y_2$?

I would treat everything constant but $y_2$ and carry out the differentiation as usual w.r.t. to $y_2$.

 

[PeroK]

I would treat everything constant but $y_2$ and carry out the differentiation as usual w.r.t. to $y_2$.

What about the function:$$G(x_1, x_2, x_3) = \frac{\rho}{x_1^2 + y_1^2 + z_1^2}$$
How would you differentiate that with respect to $y_2$?

 

[Adesh]

What about the function:$$G(x_1, x_2, x_3) = \frac{\rho}{x_1^2 + y_1^2 + z_1^2}$$
How would you differentiate that with respect to $y_2$?

It doesn’t depend on $y_2$ therefore the whole expression will act as a constant and hence the derivative will be zero.
Oh My God!

 

[archaic]

I have understood from your post is that $x$ is any arbitrary point on $\phi$ axis and $x’$ is also an arbitrary point on $\phi$ axis.

The $x$-axis or ($\varphi$-axis, call it whatever) is but a way of representing $\mathbb{R}$.
In $n$-dimensional problems, we naturally think of $n$ axes orthogonal to each other. This same concept is mathematically described using the vector space of dimension $n$, $\mathbb{R}^n$. Vector spaces have a (there is not necessarily just one) set of vectors (contained in that vector space), called a base of that vector space, whose combination ($\alpha_1\vec e_1+...+\alpha_n\vec e_n$) can give you every other vector in that vector space, and the vectors cannot be added with the coefficient $1$ to get the zero vector ($\vec e_1+...+\vec e_n\neq\vec 0$). In your case, i.e a 2D problem, we use the vector space $\mathbb{R}^2$ and the base consisting of the vectors $(1,0)$ and $(0,1)$.
Whenever you learn linear algebra, I think you'll think of these a bit differently.

 

[archaic]

Sir, please explain what does it mean to differentiate something w.r.t. to xxx.

You let $x$ vary a variation that tends to $0$, i.e $x+h$ as $h\to0$, and use the normal definition. We think of it as a tiny segment on a line, but that is just how we geometrically imagine the set of real numbers.
Keep in mind that I am a student as you are and prone to error. I'm just sharing the way I see some things and gladly would welcome a correction if I am at some point mistaken.

 

[Adesh]

The $x$-axis or ($\varphi$-axis, call it whatever) is but a way of representing $\mathbb{R}$.
In $n$-dimensional problems, we naturally think of $n$ axes orthogonal to each other. This same concept is mathematically described using the vector space of dimension $n$, $\mathbb{R}^n$. Vector spaces have a (there is not necessarily just one) set of vectors (contained in that vector space), called a base of that vector space, whose combination ($\alpha_1\vec e_1+...+\alpha_n\vec e_n$) can give you every other vector in that vector space, and the vectors cannot be added with the coefficient $1$ to get the zero vector ($\vec e_1+...+\vec e_n\neq\vec 0$). In your case, i.e a 2D problem, we use the vector space $\mathbb{R}^2$ and the base consisting of the vectors $(1,0)$ and $(0,1)$.
Whenever you learn linear algebra, I think you'll think of these a bit differently.

So, what’s the difference between differentiating with respect to $x$ and $x’$ ?

 

[PeroK]

So, what’s the difference between differentiating with respect to $x$ and $x’$ ?

The same difference as differentiating with respect to $y_1$ and $y_2$ in the above examples.

 

[Adesh]

The same difference as differentiating with respect to $y_1$ and $y_2$ in the above examples.

That solves my whole problem. Thank you so much.

 

[archaic]

So, what’s the difference between differentiating with respect to $x$ and $x’$ ?

In that response I was trying to illustrate to you the way we think of axes, but:
Define $\vec a=f(x)\vec e_1=(f(x), 0)$ and $\vec c=g(x')\vec e_1=(g(x'),0)$. You know how to do differentiation on vectors as you are reading Griffith's book, so what do you think?

That solves my whole problem. Thank you so much.

I think the main point that you need to remember is to think of the axes as the set of real numbers. The function you have of both $x$ and $x'$ who are on the same "axis" can be seen as $\vec a = f(x, x')\vec e$.

 

[mitochan]

On #4
$$\nabla\times J=[\frac{\partial J_y(x',y',z')}{\partial z}-\frac{\partial J_z(x',y',z')}{\partial y}]\hat x + ...$$
is zero.