Why heat PDE solution does not fully satisfy initial conditions?

[ujo142]

Homework Statement

Solving heat equation with internal heat cources

Relevant Equations

u_{t} = u_{xx} + q(x)/P,

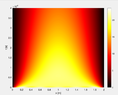
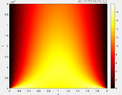
Hi, I am solving heat equation with internal heat sources both numerically and analytically. My graphs are nearly identical but! analytical one have problem at the beginning and at the end for my domain. Many people have used the same technique to solve it analytically and they got good answers. Example solution from my professor had the same issue. I cannot ask him at this time, university is closed in this week. Does anyone have at least idea what is causing this problem and how to solve it? I came up with an idea that i have some kind of tradeoff between initial and boundary conditions.

Problem: u_{t} = u_{xx} + q(x)/P, q(x) = (-x^2+2x), P=const, x: [0,L], t: [0, 40000]

u(0,t) = u(L,t) = 0 u(x, 0) = T0 = 20U can see that analytical solution does not have 20*C close to edges with small time.

 

[MathematicalPhysicist]

There's a solution through Duhamel's principle:
https://en.wikipedia.org/wiki/Duhamel's_principle

without showing us your code how can we tell?

 

[ujo142]

There's a solution through Duhamel's principle:
https://en.wikipedia.org/wiki/Duhamel's_principle

without showing us your code how can we tell?

Hi, thanks u for reply. I am not sure how showing my MATLAB code could help here. I checked several times if i correctly applied the formula. My problem is rather the formula that i derived analytically. When i put solution to equation it satisfies it. But when i just put t=0 to solution i don't get T0 as i should.

To be more precise i have solved this equation with those setps:

assume that i have solution in form u(x,t) = w(x,t) +v(x).
Then i put this into equation and got two equations:
a*w_{xx} = w_{t}
a*v_{xx} = -q/PNext i have solved first equation using separable method w(x,t)=X(x)T(t). Puting boundary conditions I got:
w(x,t) = sum_{n=1}^{inf} A_{n}sin(n*pi*x/L)*e^{-an^2pi^2t/L^4}For v(x) i got:
v(x) = P/(12a)[x^4 -2Lx^3+xL^3]So now i can put this together and got:
u(x,t) = v(x) + w(x,t) = P/(12a)[x^4 -2Lx^3+xL^3] + sum_{n=1}^{inf} A_{n}sin(n*pi*x/L)*e^{-an^2pi^2t/L^4}

Now its time to put initial conditions u(x, 0) = T0 = v(x) + w(x,0). So i have:
w(x,0) = T0 - v(x)

sum_{n=1}^{inf} A_{n}sin(n*pi*x/L)*e^{-an^2pi^2t/L^4} = T0 - P/(12a)[x^4 -2Lx^3+xL^3]

Now i have multiplied this by sinus(m*pi*x/L) and inegrated from 0 to L.
On the left side the integral is L/2*cronecker delta_{nm} and on the right there is large integral.

I calculated first 10 terms and implemented this in matlab. Is this approach correct?

 

[wrobel]

Homework Statement:: Solving heat equation with internal heat cources
Relevant Equations:: u_{t} = u_{xx} + q(x)/P,

U can see that analytical solution does not have 20*C close to edges with small time.

why do you expect that when your boundary conditions are zero?

 

[ujo142]

why do you expect that when your boundary conditions are zero?

For two reasons:
1. Numerical solution near edges is close to 20*C
2. Initial condition is 20*C for x belongs to (0,L)

 

[wrobel]

Since the initial conditions do not satisfy the boundary ones the solution is not regular as $t\to 0+$
I think you have only $\|u(t,\cdot)-u(0,\cdot)\|_{L^2(0,L)}\to 0$ as $t\to 0+$

 

[vela]

I'd guess it's that you just need to evaluate more terms. Try plotting the analytical solution u(x,0) vs. x for different number of terms in the series. I think you'll see as you increase the number of terms, the closer you get to satisfying the boundary condition.

 

[ujo142]

I'd guess it's that you just need to evaluate more terms. Try plotting the analytical solution u(x,0) vs. x for different number of terms in the series. I think you'll see as you increase the number of terms, the closer you get to satisfying the boundary condition.

Yeah, that was my problem. After 150 terms there were excellent results.