- #1
aerograce
- 64
- 1
I encountered this statement on my lecture notes today,
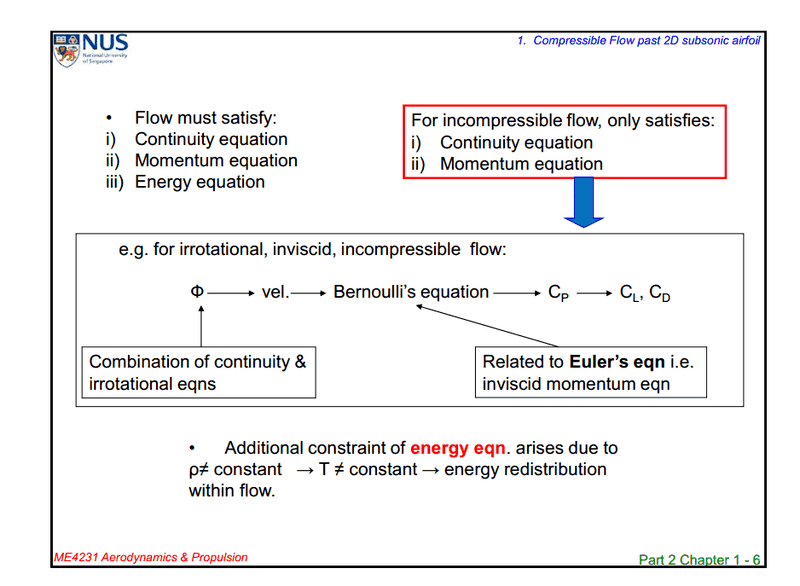
I don't understand why compressible flow needs to have another constraint of energy equation while incompressible flow only satisfies continuity and momentum equation. And how is this energy equation related to the speed of sound?
I don't understand why compressible flow needs to have another constraint of energy equation while incompressible flow only satisfies continuity and momentum equation. And how is this energy equation related to the speed of sound?