zenterix
- 774
- 84
- Homework Statement
- What exactly does it mean to say that "the magnetic field at a point ##r>>R## due to a current ring of radius ##R## may be approximated by a small magnetic dipole moment placed at the origin"?
- Relevant Equations
- ##\vec{B}=\frac{\mu_0}{4\pi} \frac{Id\vec{s}\times\hat{r}}{r^2}##
The following is from Appendix I of these notes from MIT OCW.
Consider a circular loop of radius ##R## lying in the ##xy##-plane and carrying a steady current ##I##.
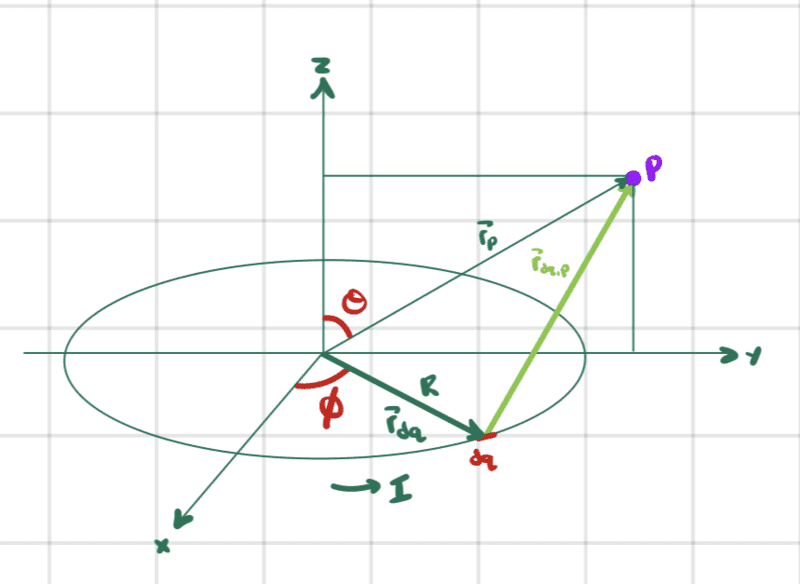
If we compute the magnetic field at a point ##P## off the axis of symmetry in the ##yz##-plane we arrive at integrals that can only be computed numerically
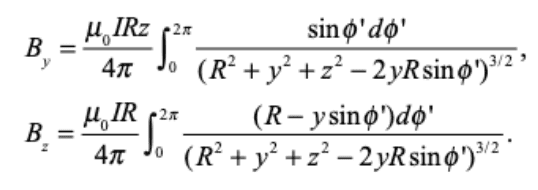
Note that the ##x##-component of ##\vec{B}## at ##P## is ##0## by symmetry.
Consider a scenario in which ##R<<(y^2+z^2)^{1/2}=r##. That is, the radius of the ring of current is much smaller than the distance to the field point ##P##.
Using linear approximation for the denominator in the expressions for ##B_y## and ##B_z## above, we reach
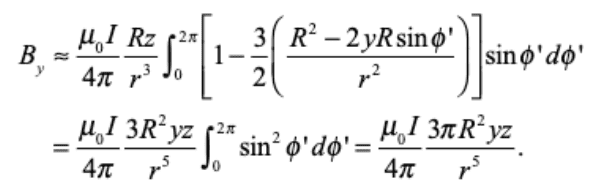
and

The notes I am reading say
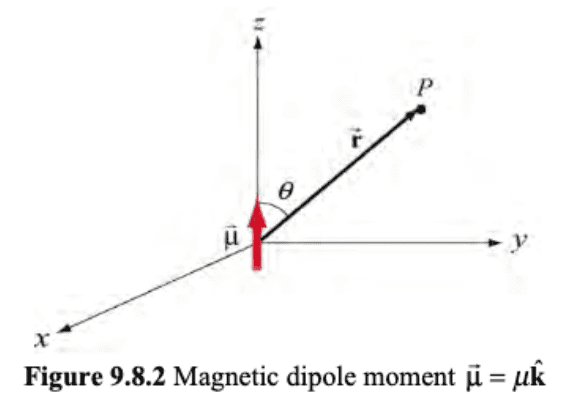
Using spherical coordinates, with ##y=r\sin{\theta}## and ##z=r\cos{\theta}## we can rewrite the expressions above as
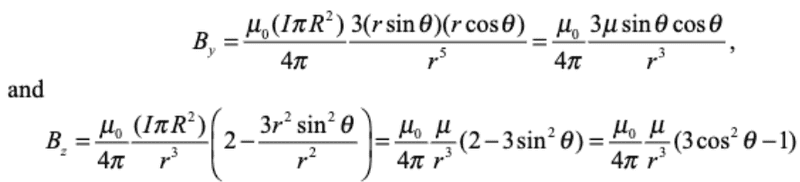
Finally, the notes say
I really do not understand the concept of a magnetic dipole very well.
Here is what I think I grasp so far
1) A magnetic dipole is a current loop.
2) The magnetic dipole moment is a vector normal to the surface enclosed by the loop (using right-hand rule relative to the current) and has magnitude ##IA##.
$$\mu=IA\hat{n}$$
3) The field of a magnetic dipole resembles that of a bar magnet. The bar magnet is also referred to as a magnetic dipole.
Ok, we have these three things for our current ring. 3) is a descriptive reason why we would say that the current ring behaves like a magnetic dipole.
But how do we see this in the equations shown above?
The expressions for ##B_y## and ##B_y## contain a ##\mu## factor in them (but also many other factors). How does this show that we can approximate the ring as a magnetic dipole moment?
Consider a circular loop of radius ##R## lying in the ##xy##-plane and carrying a steady current ##I##.
If we compute the magnetic field at a point ##P## off the axis of symmetry in the ##yz##-plane we arrive at integrals that can only be computed numerically
Note that the ##x##-component of ##\vec{B}## at ##P## is ##0## by symmetry.
Consider a scenario in which ##R<<(y^2+z^2)^{1/2}=r##. That is, the radius of the ring of current is much smaller than the distance to the field point ##P##.
Using linear approximation for the denominator in the expressions for ##B_y## and ##B_z## above, we reach
and
The notes I am reading say
The quantity ##I(\pi R^2)## may be identified as the magnitude of the magnetic dipole moment ##\mu=IA## where ##A=\pi R^2## is the area of the loop.
Using spherical coordinates, with ##y=r\sin{\theta}## and ##z=r\cos{\theta}## we can rewrite the expressions above as
Finally, the notes say
Thus, we see that the magnetic field at a point ##r>>R## due to a current ring of radius ##R## may be approximated by a small magnetic dipole moment placed at the origin
I really do not understand the concept of a magnetic dipole very well.
Here is what I think I grasp so far
1) A magnetic dipole is a current loop.
2) The magnetic dipole moment is a vector normal to the surface enclosed by the loop (using right-hand rule relative to the current) and has magnitude ##IA##.
$$\mu=IA\hat{n}$$
3) The field of a magnetic dipole resembles that of a bar magnet. The bar magnet is also referred to as a magnetic dipole.
Ok, we have these three things for our current ring. 3) is a descriptive reason why we would say that the current ring behaves like a magnetic dipole.
But how do we see this in the equations shown above?
The expressions for ##B_y## and ##B_y## contain a ##\mu## factor in them (but also many other factors). How does this show that we can approximate the ring as a magnetic dipole moment?
Last edited: