- #1
sams
Gold Member
- 84
- 2
In Chapter 8: Central-Force Motion, in the Classical Dynamics of Particles and Systems book by Thornton and Marion, Fifth Edition, page 323, Problem 8-5, we are asked to show that the two particles will collide after a time ##\tau/4√2##.
I don't have any problems with the derivations and with the integrations, but I want to know please why the authors put a negative sign in Equation (6) and what do they mean that the negative sign was included due to the fact that the time increases as the distance decreases?
Thanks a lot for your help...
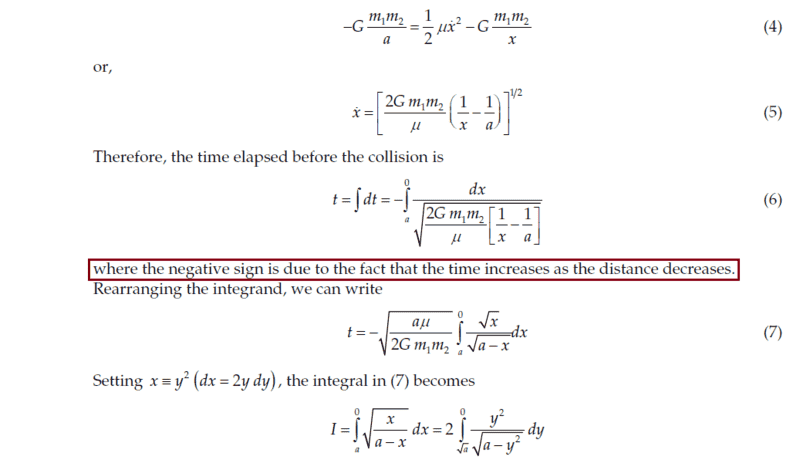
I don't have any problems with the derivations and with the integrations, but I want to know please why the authors put a negative sign in Equation (6) and what do they mean that the negative sign was included due to the fact that the time increases as the distance decreases?
Thanks a lot for your help...
