member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,
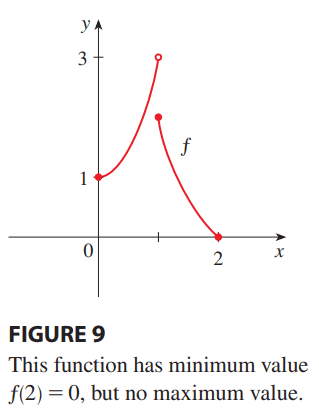
Why cannot we say that ##f(2.999999999) ≥ f(x)## and therefore absolute max at f(2.99999999999999) (without reasoning from the extreme value theorem)?
Many thanks!
Why cannot we say that ##f(2.999999999) ≥ f(x)## and therefore absolute max at f(2.99999999999999) (without reasoning from the extreme value theorem)?
Many thanks!