Why is ln(x) Important in Mathematical Formulas?

[Newtons Apple]

Hey folks...Ok so I have another question related to e and it's use in the natural log function, ln. I notice that the function ln() is used in things like the rocket equation, describing velocity of an object as it moves and uses fuel etc.. But glossing over that I'm just more curious as to why ln and more specifically it's 'e' base, is being used. Why does the value of e specicfically here apply? Furthermore why is ln at all being applied here? My overall question is..I get the value of 'e' for things like compounding interest...but when it comes to things like motion and other area's I don't see how it applies? What is it that ln will provide here? what if you used a different log ?

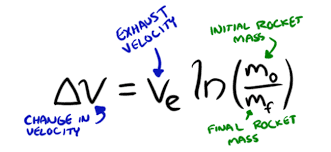
Thanks for any hints guys.. I'm just curious as to what ln is doing here and what the point of it is... Again I get that it's the natural log, and that it's base is 'e'. So it gets the value of, what number do you raise 'e' to, to get initial mass divided by final mass...but what is that important?

 

[Orodruin]

The rocket equation results from solving a differential equation. This differential equation is based on conservation of momentum and in the linit of infinitesimally small packages of exhaust. Its solution is in terms of the natural logarithm.

In the end, it all boils down to $e^x$ being its own derivative.

 

[fresh_42]

Here is my answer to it:
https://www.physicsforums.com/threads/core-of-eulers-equation.962918/#post-6108873

physics → differential equations → prototype: $y'=y$ → $y=c e^x$ and $y(0)=1$ yields the Euler number as basis

 

[haushofer]

In a lot of processes, the change in a quantity is proportional to the quantity itself. Think e.g. about the probability that you wreck your dearly-beloved China of your mother-in-law: the more se has of it, the higher the probability you drop one of her plates during doing the dishes. Or think about populations: the more humans we have, the more interactions there can be, and the more reproduction we will have. Up to a certain limit in reality, of course.

So that's what we call "exponential growth": the change of a quantity is proportional to the quantity itself. Mathematically, the function which satisfies this property is the exponential function (hence the name). It's inverse is the logarithm.

 

[Newtons Apple]

Thanks for the replies everyone! I really appreciate it.. I'm only part way through calculus I so some of this is indeed a bit lost on me... but let me try to rephrase what you're saying...and you tell me if I have it right...

So..
ln m₀/m_f

We find what the number e needs to be raised to, to get:

m₀/m_f

So if we have

m₀ = 400 and m₀/m_f = 100 ...

We get ln(4) which is : 1.39... So

e^1.39 correct?

But..what am I looking at here? What value does this have? What is this e^1.39 telling us?

 

[fresh_42]

But..what am I looking at here? What value does this have? What is this e1.39 telling us?

Nothing. In the end it is a matter of scaling, same as units are. But if we agree on natural units like $c=\hbar=G=1$ we should as well consider $y(0)=1$ as natural condition. It makes sense, since differentiation is the process of locally turning something multiplicative ($1$) into something additive ($0$). Other conditions which result in a different base, i.e. scaling factors $\log b$ are far more artificial - same as 300,000 km/s is.

 

[Newtons Apple]

Thanks for the answers but I think I found the answer more akin to what I was looking for:

There’s a fresh, intuitive explanation: The natural log gives you the time needed to reach a certain level of growth.

as well as;

So e is not an obscure, seemingly random number. e represents the idea that all continually growing systems are scaled versions of a common rate.

https://betterexplained.com/articles/demystifying-the-natural-logarithm-ln/

 

[lavinia]

Thanks for the answers but I think I found the answer more akin to what I was looking for:

There’s a fresh, intuitive explanation: The natural log gives you the time needed to reach a certain level of growth.

as well as;

So e is not an obscure, seemingly random number. e represents the idea that all continually growing systems are scaled versions of a common rate.

https://betterexplained.com/articles/demystifying-the-natural-logarithm-ln/

This link is not rigorous. The idea it gives of continuous growth is vague. Things can grow continuously in many ways not only exponentially. Post #4 gives the right answer.

The link you gave says

"Given how the natural log is described in math books, there’s little “natural” about it: it’s defined as the inverse of e^x, a strange enough exponent already."

The author then goes on to show that the log is the inverse of the exponential.