Why is m*dv/dt 0 in the Falling Chain Problem?

[al_9591]

Homework Statement

A chain of total mass M and length l is suspended vertically with
its lowest end touching a scale. The chain is released and falls onto
the scale.
What is the reading of the scale when a length of chain, x, has
fallen? (Neglect the size of individual links.)

Relevant Equations

F = dp/dt
F = ma

I have seen the solution for this problem but still there are some things I do not understand and would like clarification.
In the equations below I understand that we use the chain rule on m and v but what I don't understand why m*dv/dt is 0, I don't think is because the acceleration of dm is 0, since I assume dm is free-falling then it has acceleration g.

Also, when I tried solving for the speed of a segment of chain dm using conservation of energy, I got for v = sqrt(2gx), which is correct based on the solution I saw, but could we use for the height displaced L-x, instead of x? I tried to solve it with L-x but I got the wrong solution. My assumption here was that an element dm located at a height L-x from the floor/scale starts from rest and reaches the speed below.

 

[PeroK]

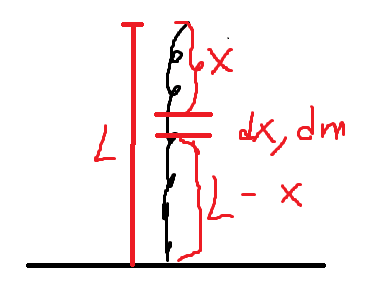
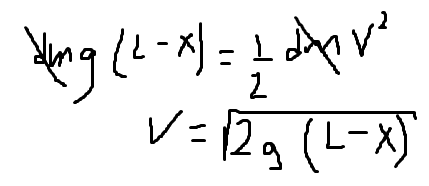
In the equations below I understand that we use the chain rule on m and v but what I don't understand why m*dv/dt is 0, I don't think is because the acceleration of dm is 0, since I assume dm is free-falling then it has acceleration g.

View attachment 278854

I don't understand that either, but then I don't accept that mass can change in Newtonian mechanics, so I don't accept the equation $F = v\frac{dm}{dt} + m\frac{dv}{dt}$.

Instead, I would consider a small time interval $\Delta t$. The mass of chain that hits the grounds in that time is proportional to the speed of the chain: $$\Delta m = \frac{M}{L}\Delta l = \frac{M}{L} v \Delta t$$
And the momentum of that small mass of chain is: $$\Delta p = v \Delta m = \frac{M}{L} v^2 \Delta t$$ hence
$$\frac{\Delta p}{\Delta t} = \frac{M}{L} v^2$$

Also, when I tried solving for the speed of a segment of chain dm using conservation of energy, I got for v = sqrt(2gx), which is correct based on the solution I saw, but could we use for the height displaced L-x, instead of x? I tried to solve it with L-x but I got the wrong solution. My assumption here was that an element dm located at a height L-x from the floor/scale starts from rest and reaches the speed below.

View attachment 278855View attachment 278856

You are given $x$ as the length of chain that has fallen. Why change that round?

 

[haruspex]

I agree with @PeroK that d(mv)/dt=vdm/dt+mdv/dt is better avoided. Too often it is misapplied.
To use it correctly, one must first specify clearly what the system is. In the extract quoted, it is the portion of chain at rest, so dv/dt is zero.
The mass being gained, dm/dt, arrives with velocity v (=v(t)), so it requires a force vdm/dt to bring it to rest.

 

[al_9591]

I don't understand that either, but then I don't accept that mass can change in Newtonian mechanics, so I don't accept the equation $F = v\frac{dm}{dt} + m\frac{dv}{dt}$.

Instead, I would consider a small time interval $\Delta t$. The mass of chain that hits the grounds in that time is proportional to the speed of the chain: $$\Delta m = \frac{M}{L}\Delta l = \frac{M}{L} v \Delta t$$
And the momentum of that small mass of chain is: $$\Delta p = v \Delta m = \frac{M}{L} v^2 \Delta t$$ hence
$$\frac{\Delta p}{\Delta t} = \frac{M}{L} v^2$$
You are given $x$ as the length of chain that has fallen. Why change that round?

Some problems I don't understand well, I usually try to solve them in different ways, this helps my understanding of the problem that is why I wanted to use L-x. Anyway, thanks for your approach on this problem, it helped me look at it from another perspective.

 

[al_9591]

I agree with @PeroK that d(mv)/dt=vdm/dt+mdv/dt is better avoided. Too often it is misapplied.
To use it correctly, one must first specify clearly what the system is. In the extract quoted, it is the portion of chain at rest, so dv/dt is zero.
The mass being gained, dm/dt, arrives with velocity v (=v(t)), so it requires a force vdm/dt to bring it to rest.

Thanks for your reply. Just out of curiosity what would be the right system? I understand that dv/dt is zero because it refers to the resting piece of chain on the table. If the part v*dm/dt is the force required to stop the piece dm, then the equation d(mv)/dt=vdm/dt+mdv/dt takes into account both, already, the piece on the floor and the falling dm piece. If this is so, we shouldn't need to add the force done by the floor also, as this one is considered in the equation d(mv)/dt=vdm/dt+mdv/dt already , is this correct?

 

[haruspex]

we shouldn't need to add the force done by the floor also, as this one is considered in the equation

Not sure what you mean by that.
The conceptual difficulty is the representation of the force required to stop the falling dm of chain.
You can consider the dm to exert an external force acting on the system consisting of the resting mass m, balanced by gravity (mg) and the normal force from the ground:
$F_{net}=F_{normal}+mg+v\frac{dm}{dt}=\frac{dp}{dt}=0$ (taking down as positive everywhere).
Or, you can consider the mass on the ground and the added dm as the system, undergoing a momentum change vdm each dt:
$F_{net}=F_{normal}+mg=\frac{dp}{dt}=-v\frac{dm}{dt}$.