- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading Andrew McInerney's book: First Steps in Differential Geometry: Riemannian, Contact, Symplectic ... and I am focused on Chapter 3: Advanced Calculus ... and in particular on Section 3.1: The Derivative and Linear Approximation ...
In Section 3.1 McInerney defines what is meant by a function ##f: \mathbb{R}^n \to \mathbb{R}^m## being differentiable and also defines the derivative of f at a point ##a \in \mathbb{R}^n## ...
... see the scanned text below for McInerney's definitions and notation ...
... McInerney then gives several examples ... I need help with several aspects of Example 3.1.5 which reads as follows:
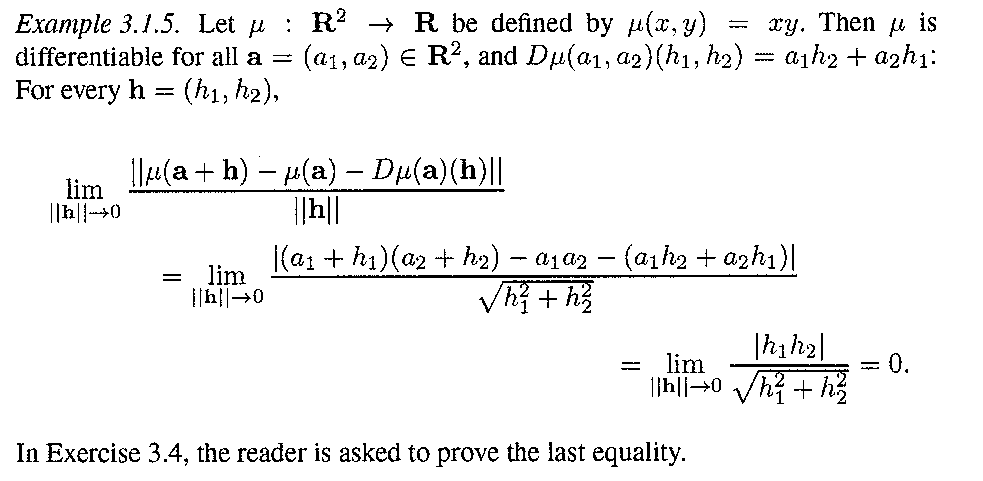
I have two questions with respect to Example 3.1.5 ...Question 1
In the above text from McInerney we read the following:
"... ... Then ##\mu## is differentiable for all ##a = (a_1, a_2) \in \mathbb{R}^2## and ##D \mu (a_1, a_2) (h_1, h_2) = a_1 h_2 + a_2 h_1 ## ... ..Can someone explain exactly how/why ...
(a) ##\mu## is differentiable for all ##a = (a_1, a_2) \in \mathbb{R}^2## ... ...
and ...
(b) ##D \mu (a_1, a_2) (h_1, h_2) = a_1 h_2 + a_2 h_1 ## ... .. that is how/why is this true ...
(especially given that McInerney has only just defined differentiable and the derivative!)Question 2
In the above text from McInerney we read the following:
"... ... ##\displaystyle \lim_{ \mid \mid h \mid \mid \to 0} \frac{ \mid h_1 h_2 \mid }{ \sqrt{ h_1^2 + h_2^2 } } = 0 ##... ...Can someone please show and explain exactly how/why it is that ##\displaystyle \lim_{ \mid \mid h \mid \mid \to 0} \frac{ \mid h_1 h_2 \mid }{ \sqrt{ h_1^2 + h_2^2 } } = 0## ... ...
Help will be much appreciated ... ...
Peter============================================================================================================================
It may help members reading the above post to have access to the text at the start of Section 3.1 of McInerney ... if only to give access to McInerney's terminology and notation ... so I am providing access to the text at the start of Section 3.1 ... as follows:
 Hope that helps ...
Hope that helps ...
Peter
In Section 3.1 McInerney defines what is meant by a function ##f: \mathbb{R}^n \to \mathbb{R}^m## being differentiable and also defines the derivative of f at a point ##a \in \mathbb{R}^n## ...
... see the scanned text below for McInerney's definitions and notation ...
... McInerney then gives several examples ... I need help with several aspects of Example 3.1.5 which reads as follows:
I have two questions with respect to Example 3.1.5 ...Question 1
In the above text from McInerney we read the following:
"... ... Then ##\mu## is differentiable for all ##a = (a_1, a_2) \in \mathbb{R}^2## and ##D \mu (a_1, a_2) (h_1, h_2) = a_1 h_2 + a_2 h_1 ## ... ..Can someone explain exactly how/why ...
(a) ##\mu## is differentiable for all ##a = (a_1, a_2) \in \mathbb{R}^2## ... ...
and ...
(b) ##D \mu (a_1, a_2) (h_1, h_2) = a_1 h_2 + a_2 h_1 ## ... .. that is how/why is this true ...
(especially given that McInerney has only just defined differentiable and the derivative!)Question 2
In the above text from McInerney we read the following:
"... ... ##\displaystyle \lim_{ \mid \mid h \mid \mid \to 0} \frac{ \mid h_1 h_2 \mid }{ \sqrt{ h_1^2 + h_2^2 } } = 0 ##... ...Can someone please show and explain exactly how/why it is that ##\displaystyle \lim_{ \mid \mid h \mid \mid \to 0} \frac{ \mid h_1 h_2 \mid }{ \sqrt{ h_1^2 + h_2^2 } } = 0## ... ...
Help will be much appreciated ... ...
Peter============================================================================================================================
It may help members reading the above post to have access to the text at the start of Section 3.1 of McInerney ... if only to give access to McInerney's terminology and notation ... so I am providing access to the text at the start of Section 3.1 ... as follows:
Peter
Attachments
Last edited: