Why Is My Acceleration Calculation Not Matching the Expected Result?

[Bashyboy]

Homework Statement

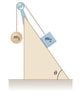
Two objects are connected by a light string that passes over a friction less pulley as shown in the figure below. Assume the incline is friction less and take m1 = 2.00 kg, m2 = 7.75 kg, and θ = 55.5°.

From this information, I have to determine the acceleration and tension of the string.

Homework Equations

The Attempt at a Solution

I attached the diagram and my work as files.

I used the last formula to find the acceleration. I plugged in the values, and got a = \frac{7.75cos(34.5)-2.00(-9.8)}{2.00+7.75}, which simplifies to 2.67 m/s^2. The actual answer is 4.41 m/s^. Can anyone account for this difference?

 

[frogjg2003]

You lost a g in the first equation below thewavy line. Look at the equations in the post:
\frac{7.75kg*cos(34.5^\circ)-2.00kg(-9.8m/s^2)}{2.00kg+7.75kg}. You can't add kg and N.

 

[Bashyboy]

Oh, so it's suppose to be mgcos(34.5)?

 

[Bashyboy]

Also, how do I know when acceleration due to gravity is positive or negative?

 

[Bashyboy]

For instance, there is an example problem involving an Atwood Machine, with mass 1(m1) having less mass than mass two (m2). The author defines the upward direction as positive for m1, and the downward direction as positive for m2. Isn't downward and upward point in opposite directions? So, shouldn't one of them be a negative direction, and the other be a positive direction? Why are we allowed to define upwards and downwards as both being positive directions?

 

[frogjg2003]

First off, g will always be positive, it's the geometry that determines whether you would use g, -g, g cos($\theta$), g sin($\theta$). As for which direction is positive and which direction is negative, it is fairly arbitrary. In your problem, and in an Atwood machine, the only requirement is that the velocities of the two masses are the same and in the correct direction. That is because the string is assumed to not change length. Everything else is just making sure your equations are correctly set up.

 

[Bashyboy]

So, I can basically think of each mass having a coordinate system with its origin placed at the center of the mass; so that each mass has its own coordinate system? Also, should I always choose the direction of the acceleration to be positive?

 

[frogjg2003]

No. By using the center of mass of the object (which is accelerating) as the origin, you've created a non-inertial frame. You're close though. In these kinds of problems, you should think of it as two coordinate systems. The first is for the hanging mass. The other is the mass on a slope (or second hanging mass in an Atwood machine). The unstretchable string sets up the condition that any change of position in one coordinate system produces an analogous change in the second. If you have positive to be up in the hanging frame, then positive should be down-slope in the sloped frame, because moving the hanging mass up will move the slope mass down. Same goes for velocity and acceleration. If you have a downward acceleration in the hanging frame, you need an acceleration up the slope in the sloped frame.

It's convenient to have a be positive always, but it's not necessary, and the physics doesn't change if you come out with a negative acceleration. It just means that the acceleration was in the opposite direction from what you called positive.

 

[nasu]

Oh, so it's suppose to be mgcos(34.5)?

Besides the observations made by frogjg2003, see that the angle in your drawing is not the same as shown in the problem. So even after correcting these issues, you won't get the same answer as in the book. What you label by "θ" is the complement of the θ in the original figure.