- #1
The Real Nick
- 25
- 0
MODERATOR'S NOTE: THIS THREAD HAS BEEN MOVED FROM ANOTHER FORUM, SO THERE IS NO TEMPLATE.
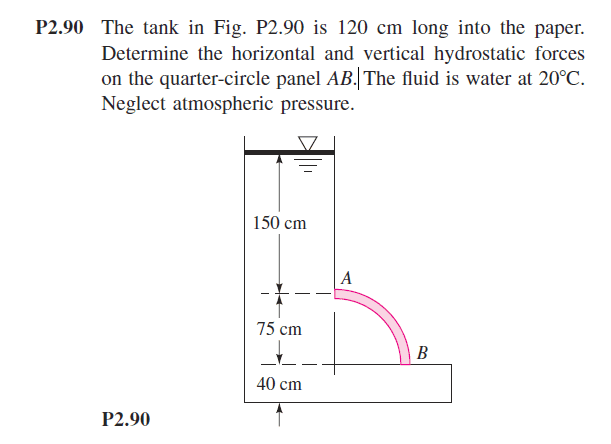
This is the problem here. I am having trouble making progress on this problem after getting the wrong answer for the vertical hydrostatic force.
The equations I am using are: fx= (density)(gravity)(Zcg)(Projected area)
For this I used
p= 1000 kg/m^3
g = 9.81 m/s^2
Zcg = 1.5m + (0.75/2)m
A = (0.75(1.2) m^2
this gave me 16,554.4 N, which is correct (for the horizontal component).
Now, trying to solve for the vertical hydrostatic force I used the same equation, but with Zcg being 1.5+0.75 meters as it is at the bottom of the quarter-circle. I am not sure what else to do, but this doesn't give me the right answer, it is short by about 3,000 N.
I have seen other solutions that solve for the vertical force by finding the "weight of the missing water" above the quarter-circle. I don't understand this method, and it was never explained in class or in my book, so I am weary to use it.
If anyone could help that would be great!
Thank you.
This is the problem here. I am having trouble making progress on this problem after getting the wrong answer for the vertical hydrostatic force.
The equations I am using are: fx= (density)(gravity)(Zcg)(Projected area)
For this I used
p= 1000 kg/m^3
g = 9.81 m/s^2
Zcg = 1.5m + (0.75/2)m
A = (0.75(1.2) m^2
this gave me 16,554.4 N, which is correct (for the horizontal component).
Now, trying to solve for the vertical hydrostatic force I used the same equation, but with Zcg being 1.5+0.75 meters as it is at the bottom of the quarter-circle. I am not sure what else to do, but this doesn't give me the right answer, it is short by about 3,000 N.
I have seen other solutions that solve for the vertical force by finding the "weight of the missing water" above the quarter-circle. I don't understand this method, and it was never explained in class or in my book, so I am weary to use it.
If anyone could help that would be great!
Thank you.
Last edited by a moderator: