Why is ##\text{flux} = \pi\text{intensity}##

[yucheng]

Homework Statement

N/A

Relevant Equations

N/A

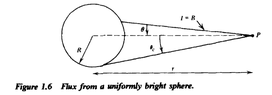
Textbook Derivation
Flux at an arbitrary distance from a sphere of uniform brightness $B$ (that is, all rays leaving the sphere have the same brightness). Such a sphere is clearly an isotropic source. At $P$, the specific intensity is $B$ if the ray intersects the sphere and zero otherwise (see Fig. 1.6). Then,
$$
F=\int I \cos \theta d \Omega=B \int_{0}^{2 \pi} d \phi \int_{0}^{\theta_{c}} \sin \theta \cos \theta d \theta
$$
where $\theta_{c}=\sin ^{-1} R / r$ is the angle at which a ray from $P$ is tangent to the sphere. It follows that
$$
F=\pi B\left(1-\cos ^{2} \theta_{c}\right)=\pi B \sin ^{2} \theta_{c}
$$
or
$$
F=\pi B\left(\frac{R}{r}\right)^{2}
$$

Setting $r=R:$
$$
F=\pi B
$$
That is, the flux at a surface of uniform brightness $B$ is simply $\pi B$.

My worries
1. How is the equation valid when $r=R$? The author made an approximation that $\theta_{c}=\sin ^{-1} R / r$, and r is not the hypotenuse of the triangle, hence the approximation is only valid when $r >> R$ or $\text{leg} \approx hypotenuse$. Rather, r is a leg. In this case, doesn't the approximation fail and vitiate the result that $F=\pi B$?

2. Actually, which case does $r=R$ refer to? Diagram 2 or 3 below?



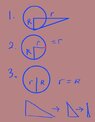
3. Is there a physical interpretation/explanation for $F=\pi B$? The way I would think of it is that $\pi$ represents the patch of the sphere where the point resides (it is 1/4 of the whole sphere) and that this whole patch contributes to the flux at that point.

 

[haruspex]

r is not the hypothenuse of the triangle

Looks like the hypotenuse to me.
You must have the wrong triangle.
The R is from the sphere's centre to where the tangent from P touches the sphere. It makes a right angle to that tangent, not to r.

 

[yucheng]

Looks like the hypotenuse to me.
You must have the wrong triangle.
The R is from the sphere's centre to where the tangent from P touches the sphere. It makes a right angle to that tangent, not to r.

Oops, wrong triangle indeed. So when $r \to R$? So it does become like figure 3 (In the second thumbnail), albeit a different orientation. Ah I see it. Thanks! But the interpretation of $F = \pi B$?

 

[haruspex]

But the interpretation of $F = \pi B$?

I'm not sure why it doesn't turn out to be $F = 2\pi B$. On reaching the sphere, the sphere occupies one half of what can be seen from P, so that should be a solid angle of $2\pi$.
Need to think about it some more.

 

[yucheng]

I'm not sure why it doesn't turn out to be $F = 2\pi B$. On reaching the sphere, the sphere occupies one half of what can be seen from P, so that should be a solid angle of $2\pi$.
Need to think about it some more.

Let $B_v$ be the intensity ($\text{flux} \; \text{rad}^{-1} Hz^{-1}$)

However, the amount of radiation emitted is not isotropic. It depends on the angle from the normal of the surface (or projected surface).

$$F_v = \int B_v \cos{\theta} \, d\Omega =\int^{2\pi}_{0} \int^{ \pi}_{0} B_v \cos {\theta} \sin{\theta} \, d\theta \, d\phi = \pi B_v $$

I guess this makes sense, that F is not $4\pi B$, nor is it $2\pi B$