- #1
Abu
Homework Statement
Prove that in the elastic collision of two objects of identical mass, with one being a target initially at rest, the angle between their final velocity vectors is always 90 degrees.
Homework Equations
m1v1+m2v2 = m1v1'+m2v2'
1/2m1v1^2 +1/2m2v2^2 = 1/2m1v1'^2 + 1/2m2v2'^2
v1-v2 = v2'-v1'
The Attempt at a Solution
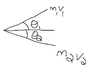
This was my attempt:
Very sloppy diagram ^^^ but it is what I was basing my equations off of.
m1 = m2 = m
Y Direction:
0 = mv1'sinθ1 - mv2'sinθ2
Cancel m's and set equal to each other
v1'sinθ1 = v2'sinθ2
Solve for v1'
v1' = v2'sinθ2/sinθ1
X Direction
mv1 + 0 = mv1'cosθ1 + mv2'cosθ2
Cancel m's
v1 = v1'cosθ1 + v2'cosθ2
Use the v1-v2 = v2'-v1' formula and sub in v1' from Y direction and v1 from x direction
v1'cosθ1 + v2'cosθ2 = v2' - v2sinθ2/sinθ1
So that's as far as I got because from there I didn't know how to simplify it further (I don't know trigonometric identities) and I didn't even think I was on the right track.
I saw from other sources that you can simply use the conservation of kinetic energy equation, cancel m's and the 1/2, and use that as pythagoras.
It was basically: 1/2mv1^2 = 1/2mv1'^2 + 1/2mv2'^2
Cancel the m's and 1/2 and you have
v1^2 = v1'^2 + v2'^2
If that method is correct, can someone explain it to me?