- #1
- 1,798
- 33
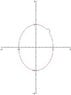
Suppose I want to integrate [tex]f(z)(z-a)^{-1}[/tex] where [tex]|a|=1[/tex] over the circle [tex]|a|=1[/tex], why is it that:
[tex]
f(a)=\frac{1}{\pi i}\int_{|z|=1}\frac{f(z)}{z-a}dz
[/tex]
instead of:
[tex]
f(a)=\frac{1}{2\pi i}\int_{|z|=1}\frac{f(z)}{z-a}dz
[/tex]
[tex]
f(a)=\frac{1}{\pi i}\int_{|z|=1}\frac{f(z)}{z-a}dz
[/tex]
instead of:
[tex]
f(a)=\frac{1}{2\pi i}\int_{|z|=1}\frac{f(z)}{z-a}dz
[/tex]