Why is the curvature around a star asymmetrical in the theory of relativity?

[udaykumar]

hello all
I am new to physics ..and i am curious about the theory of relativity.I do have little knowledge of relativity theory and space-time curvature. I think there are many who are like me and want to know abt this theory. So anybody who has relavent material that is easy to understand..please do reply with the links or discussions..ur help will be appreciated.

Need Clarification: From my understanding of the theory of relativity a large body like a star makes the space to curve and the smaller bodies like the planets revolve around the stars due to this curvature and try to get towards the star.

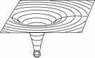
But my doubt is a body like star as it makes the curvature , should make the curvature symmetrically around itself like a globe or sphere. But why is the curvature assymetrical (as shown in the attached file) so that the smaller planets revolve around it ? If the curvature made is symmetical then the planets would not revolve around the star but would just stay where they are.

 

[neutrino]

So, if I understand you question correclty, you want to know why a planetary system doesn't look like the archetypical/classical picture of an atom, with electrons going around in orbits all around the nuclues, right?

I could be wrong, but I think it may have something to do with the rotation of the proto-star, i.e. the early stage of a star, and the formation of the proto-planetary disc.

 

[udaykumar]

Thanku for the reply,
But i think u didn't get my question correctly, my question was withrespect to theory of relativity. Theory of relativity says :
Physicist John Wheeler put it well when he said "Matter tells space how to curve, and space tells matter how to move."
That means because of the curvature made by star in space-time ..planets move around the star and finally they end up at the star. But my question is as space is everywhere ..it is symmetrical .. So star too if it makes curvature , should make it symmetrical..but from the theory of relativity , i find that the curve is not symmetrical ( it is downward ...like a ball placed on a rubber sheet) . Why is this so ? .

Please make comments if u don't understand the question.

 

[anantchowdhary]

u can hav a loook at the videos on

http://www.pbs.org/wgbh/nova/elegant/program.html

especially :A new Picture of gravity

 

[pervect]

You might want to take a look at http://www.eftaylor.com/pub/chapter2.pdf

Basically, the diagram you drew is an embedding diagram. There are other ways of looking at curvature, however. The concept of curvature can be and in GR is usually derived from the notion of intrinsic curvature, not extrinsic curvature. To measure intrinsic curvature, one measures the distances between various points on a surface. Deviations from flatness will become obvious when one tries to come up with a mathematical model that describes the value of distance between any two points.

See the link I quoted above, here is some sample text (without the diagrams):

Figure 1 Reproducing the shape of an overturned rowboat (top) by driving nails around its perimeter, then stretching strings between each nail and every nearby nail (middle). The shape of the rowboat can be reconstructed (bottom) using only the lengths of string segments—the distances between nails. To increase the precision of reproduction, increase the number of nails, the number of string segments, the table of distances.

There is a further wrinkle. In GR, it is space-time that is curved, not just space. Rather than measure distances between points, one measures the space-time interval , also known as the Lorentz interval, between events (points that also have a time coordinate, i.e. a time of occurence.)

Understanding this point in detail will require understanding special relativity. General relativity is built upon special relativity, so you won't get terribly far in GR without understanding SR first.

 

[russ_watters]

To put it another way, that diagram is a 2d sketch of a 3d representation of a 4d concept. It shouldn't be taken literally and it is impossible to actually visualize this curvature realistically.

But to answer the question, the curvature is all around the object, and you can see it's effect with gravitational lensing causing halos due to the light from distant objects wrapping completely around massive objects: http://astro.imperial.ac.uk/Research/Extragal/

 

[Pippo]

Answer to :

But my question is as space is everywhere ..it is symmetrical .. So star too if it makes curvature , should make it symmetrical..but from the theory of relativity , i find that the curve is not symmetrical ( it is downward ...like a ball placed on a rubber sheet) . Why is this so ? .



The curvature can't be symmetrical as the presence of other bodies, matters, including the observer.[/

 

[udaykumar]

"The curvature can't be symmetrical as the presence of other bodies, matters, including the observer."

But i don't think the mass of other objects like planets are taken into consideration in deriving the curvature made by star in einsteins equations..

Thanks to anantchowdhary , pervect , russ_watters and Pippo for their links, suggestions and answers .. i am in the process of learning relativity theories..hope i do succeed soon..

 

[MeJennifer]

"The curvature can't be symmetrical as the presence of other bodies, matters, including the observer."

The motions of observers and test particles, which are considered objects without mass and energy, are derived from exact solutions. Obviously no such objects or observers exist in nature. But for instance if we model the gravitational interaction between a photon and a black hole it must be obvious that the photon mass/energy is practically speaking zero in comparison with the mass/energy of the black hole.

Vacuum solutions such as the Schwarzschild and Kerr solutions do not even model interactions, for that we need at least two particles.

 

[Chris Hillman]

Attempted clarification

i am curious about the theory of relativity.I do have little knowledge of relativity theory and space-time curvature. I think there are many who are like me and want to know abt this theory. So anybody who has relavent material that is easy to understand..please do reply with the links or discussions..ur help will be appreciated.

The website in my signature offers links to educational websites on relativistic physics at a variety of levels, from popular through undergraduate, graduate, and research level.

Need Clarification: From my understanding of the theory of relativity a large body like a star makes the space to curve and the smaller bodies like the planets revolve around the stars due to this curvature and try to get towards the star.

But my doubt is a body like star as it makes the curvature , should make the curvature symmetrically around itself like a globe or sphere. But why is the curvature assymetrical (as shown in the attached file) so that the smaller planets revolve around it ? If the curvature made is symmetical then the planets would not revolve around the star but would just stay where they are.

Your thumbnail depicts a schematic version of the "Flamm paraboloid" which depicts the (spherically symmetric!) geometry of a three-dimensional spacelike hyperslice through the unique static spherically symmetric vacuum solution in gtr, the Schwarzschild vacuum solution. This slice is the one which is orthogonal to the world lines of static observers (who exist only outside the horizon, which is the locus where the embedded surface "turns vertical").

Is it possible that you misunderstood what this figure represents? This is a radially symmetric surface embedded in a flat three-dimensional space having no physical significance. The intention is that you mentally replace the concentric level circles with spheres and abstract away the embedding space. It is just a way to visualize the geometry of the hyperslice, which is three-dimensional and spherically symmetric.

Note that other families of observers may define very different "orthogonal hyperslices" (or none at all). For example, observers radially infalling from rest "at infinity" have world lines which are orthogonal to another family of three-dimensional spatial hyperslices, which again are all isometric to one another. But these are all flat! (That's pretty easy to visualize!)

(Aside to other readers: the surface in Uday's gif flattens out much too quickly to be a paraboloid--- no doubt this was the artist's attempt to suggest that the curvature goes to zero as you get far away, which might not be evident to many students viewing a more accurate embedding. This illustrates one limitation of such embedding diagrams; there are many others.)