Why is the flow rate reversing in this fuel delivery system?

[Kieran989]

Hi everyone,

I have a real life fluids problem I am trying to solve theoretically.

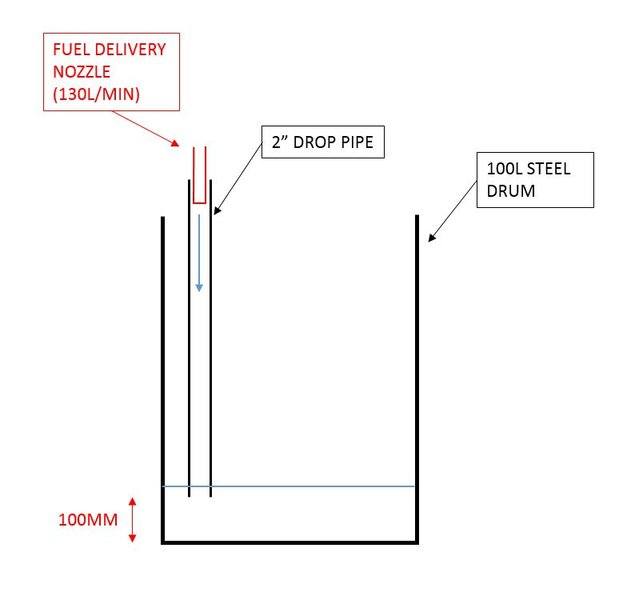
During a commissioning exercise we needed to discharge fuel into a 100L steel drum to test flow rates for a new re-fuelling skid. To minimise turbulent flow and static build up a drop pipe was used for the hose nozzle to discharge into.

The drop pipe was made from 2" pipe and suspended approx 100mm from the bottom of the drum. During the commissioning exercise, fuel was discharged into the drum via the drop pipe at a rate of 130L/min. However once the level of fluid reached the bottom of the drop pipe, the 2" pipe could not handle the flow delivery and the flow path reversed back up the drop pipe and cut out the delivery nozzle.

We have solved the issue by fabricating a new drop pipe from 3" pipe which allows the fuel to be delivered to the drum safely with no backflow concerns.

I'm hoping someone can explain this issue theoretically with a fluid diagram / Bernoulli equation etc?

See attached a diagram to better explain the scenario.

Thanks for your help. Any questions let me know

 

[Delta2]

Did you keep the same volumetric flow rate (130L/min) after you switched to the 3'' pipe? If yes then I think I have a qualitative explanation of what happened.

The atmospheric pressure plus the pressure from the weight of the fluid in the drum overcomes the pressure of the fluid in the delivery pipe. Thats why you had back flow.

When you switched to 3'' pipe while keeping the same volumetric flow rate, the velocity of the fluid in the pipe became smaller (because the vol. flow rate equals $Sv$ where S the cross area of the pipe and v the velocity of the fluid, so if $S$ becomes larger, $v$ has to become smaller in order to keep $Sv$ constant), and by Bernoulli's principle smaller velocity means bigger pressure. So the bigger pressure inside the 3'' pipe (relative to the pressure of the 2'' pipe) made it possible to successfully fill the drum.

BUT I ll just invoke kindly @Chestermiller to read this thread, who is the expert in fluid dynamics here, and to offer us his qualitative and quantitative insight.

 

[Kieran989]

Thanks Delta. Yes it was the same flow rate.

Your explanation makes some sense. Could you attempt to put numbers to the Bernoulli equation?

It was actually 1" pipe we originally used (not 2" as explained incorrectly before)

 

[Delta2]

well the velocity of the fluid in the 3'' pipe was nine times smaller than the velocity of the fluid in the 1'' pipe.

Bernulli's equation $\frac 1 2 \rho v_{1''}^2+p_{1''}=\frac 1 2 \rho v_{3''}^2 +p_{3''}$ and replacing $v_1=9v_3$ we ll get after some algebra that $p_{3''}=p_{1''}+40\rho v_{3''}^2$

If I calculated correctly $v_{3''}=0.475m/s$ based on the flow rate and the pipe diameter (is it 3 inches diameter or 3/4 inches?) . Need to know the density of the fluid to find how much was the increase in pressure due to the lower velocity inside the 3''pipe.

have in mind I am not sure at all at how I apply Bernoulli's Equation, if you want an answer as valid as possible wait for @Chestermiller to reply, he is an expert in fluid dynamics.

 

[Dullard]

I find the explanation above to be confusing - that probably has more to do with me than the explanation. I would approach the explanation from a 'discharge coefficient' POV - I don't believe that what's going on 'inside' the pipe is really the issue (there is a small difference). When the fluid is below the end of the pipe, the added liquid is discharged into the tank atmosphere. When the fluid reaches the end of the pipe, the pressure required to maintain the same flow increases (liquid is a lot harder to 'shove' out of the way) - this is a significant 'mode change.' The larger pipe has a larger exit cross-section/lower velocities - the exit dP is much smaller. The static head (essentially the same for both pipes) is sufficient to produce the required flow for the larger pipe (and not for the smaller).

 

[Delta2]

I find the explanation above to be confusing - that probably has more to do with me than the explanation. I would approach the explanation from a 'discharge coefficient' POV - I don't believe that what's going on 'inside' the pipe is really the issue (there is a small difference). When the fluid is below the end of the pipe, the added liquid is discharged into the tank atmosphere. When the fluid reaches the end of the pipe, the pressure required to maintain the same flow increases (liquid is a lot harder to 'shove' out of the way) - this is a significant 'mode change.' The larger pipe has a larger exit cross-section/lower velocities - the exit dP is much smaller. The static head (essentially the same for both pipes) is sufficient to produce the required flow for the larger pipe (and not for the smaller).

Well seems to me you are right about your qualitative analysis (indeed the liquid will be harder to shove out of the way than the plain air). I don't think I understand completely the "discharge coefficient" point of view, but anyway I am just a mathematician, don't know so much about fluid dynamics, especially regarding the qualitative understanding. Just wait kindly for Chet's reply, I am sure he ll guide you to understand this fully.

 

[Mohankpvk]

Did you keep the same volumetric flow rate (130L/min) after you switched to the 3'' pipe? If yes then I think I have a qualitative explanation of what happened.

The atmospheric pressure plus the pressure from the weight of the fluid in the drum overcomes the pressure of the fluid in the delivery pipe. Thats why you had back flow.

When you switched to 3'' pipe while keeping the same volumetric flow rate, the velocity of the fluid in the pipe became smaller (because the vol. flow rate equals $Sv$ where S the cross area of the pipe and v the velocity of the fluid, so if $S$ becomes larger, $v$ has to become smaller in order to keep $Sv$ constant), and by Bernoulli's principle smaller velocity means bigger pressure. So the bigger pressure inside the 3'' pipe (relative to the pressure of the 2'' pipe) made it possible to successfully fill the drum.

BUT I ll just invoke kindly @Chestermiller to read this thread, who is the expert in fluid dynamics here, and to offer us his qualitative and quantitative insight.

But I think Sv(mass flow rate) will not be constant between the two cases.I made the same mistake once.It seems the mass flow rate wirth respect to position(mass flow rate along the pipe) will remain constant for both the cases seperately.But when the cross section at a point changes with time, the mass flow rate will also change(as a whole throughout the pipe).Flow control valves work by this principle.

 

[Chestermiller]

I find the explanation above to be confusing - that probably has more to do with me than the explanation. I would approach the explanation from a 'discharge coefficient' POV - I don't believe that what's going on 'inside' the pipe is really the issue (there is a small difference). When the fluid is below the end of the pipe, the added liquid is discharged into the tank atmosphere. When the fluid reaches the end of the pipe, the pressure required to maintain the same flow increases (liquid is a lot harder to 'shove' out of the way) - this is a significant 'mode change.' The larger pipe has a larger exit cross-section/lower velocities - the exit dP is much smaller. The static head (essentially the same for both pipes) is sufficient to produce the required flow for the larger pipe (and not for the smaller).

I agree with this explanation, but I would like to put some numbers on it. What is the length of the drop pipe, and/or the depth of the liquid in the tank when the tank is considered full? Also, what is the diameter of the nozzle?

 

[Delta2]

But I think Sv(mass flow rate) will not be constant between the two cases.I made the same mistake once.It seems the mass flow rate wirth respect to position(mass flow rate along the pipe) will remain constant for both the cases seperately.But when the cross section at a point changes with time, the mass flow rate will also change(as a whole throughout the pipe).Flow control valves work by this principle.

Well to be honest I don't know how flow control valves work , but as long as the fluid's flow is considered to be steady (velocity at a point does not depend on time) and incompressible (density does not varies along a streamline), then the mass flow rate always remains the same between pipes with different cross section areas.

 

[Mohankpvk]

Well to be honest I don't know how flow control valves work , but as long as the fluid's flow is considered to be steady (velocity at a point does not depend on time) and incompressible (density does not varies along a streamline), then the mass flow rate always remains the same between pipes with different cross section areas.

I think it remains constant along a pipe of varying cross section area but if you change a part of the pipe with a different pipe(with a different cross section area),then the flow rate will be different.

 

[Delta2]

I think it remains constant along a pipe of varying cross section area but if you change a part of the pipe with a different pipe(with a different cross section area),then the flow rate will be different.

Ok let's say you take two pipes with different cross section areas and you merge them to one pipe. We can view this one pipe as of varying cross section area , the only difference is that there might be something like a discontinuity in the cross section area variation (at the point of merging it changes suddenly from S1 area to S2 area).

 

[Mohankpvk]

Ok let's say you take two pipes with different cross section areas and you merge them to one pipe. We can view this one pipe as of varying cross section area , the only difference is that there might be something like a discontinuity in the cross section area variation (at the point of merging it changes suddenly from S1 area to S2 area).

I think the change in flow rate will depend on the cross section area of the new pipe added.Someone in this forum explained this to me with an example.Something like two tanks(of same capacity) with water at the same height were assumed.One of the tanks had a smaller hole(can be assumed as a pipe of smaller dia) and the other had a larger hole(can be assumed as a pipe of larger dia).The discharge was allowed to start at the same time. Which tank would be empty first?
(Assume the holes to be at the bottom i.e, at the same height)

 

[Delta2]

I think the change in flow rate will depend on the cross section area of the new pipe added.Someone in this forum explained this to me with an example.Something like two tanks(of same capacity) with water at the same height were assumed.One of the tanks had a smaller hole(can be assumed as a pipe of smaller dia) and the other had a larger hole(can be assumed as a pipe of larger dia).The discharge was allowed to start at the same time. Which tank would be empty first?
(Assume the holes to be at the bottom i.e, at the same height)

The tank with the bigger diameter would be empty first(as far as I know the velocity of the fluid exit will be the same for both tanks), but I don't think this tank analogy is appropriate.

Between the two pipes, the continuity equation will force equal flow rates, as long as the flow is incompressible and steady. The two tank analogy has nothing to do with continuity equation, each tank can have different flow rate, its flow rate isn't restricted by the continuity equation.

 

[Mohankpvk]

The tank with the bigger diameter would be empty first(as far as I know the velocity of the fluid exit will be the same for both tanks), but I don't think this tank analogy is appropriate.

Between the two pipes, the continuity equation will force equal flow rates, as long as the flow is incompressible and steady. The two tank analogy has nothing to do with continuity equation, each tank can have different flow rate, its flow rate isn't restricted by the continuity equation.

Yes, the two tanks can have different flow rates.The only difference between the two tanks was the size of the outlet pipe(everything else is same).These two tanks can even be considered as the same tank at two different instances.This is similar to the case where initialy, a smaller pipe is used as outlet and then the pipe is replaced by a larger pipe(the situation mentioned in the question).So, I think between these two cases flow rate can change.

 

[Kieran989]

I agree with this explanation, but I would like to put some numbers on it. What is the length of the drop pipe, and/or the depth of the liquid in the tank when the tank is considered full? Also, what is the diameter of the nozzle?

Hi Chestermiller,

Some of the numbers i gave earlier were wrong. The drum is actually 200L and measures approx 880mm high.

The drop pipe was constructed from a 3"x1" reducer welded to a length of 1" pipe. The drop pipe was inserted into the drum opening so that the bottom of the pipe rests approx 100mm above the bottom of the drum. The reducer sits above the level of the drum and allows the nozzle to be inserted. Nozzle diameter is 38mm (approx 35mm internal dia).

Drum is considered full once it reaches approx 50mm below top surface. Not sure how this is relevant though? Backflow was occurring as soon as the level of liquid in the drum reached the bottom of the drop pipe.

 

[Chestermiller]

Hi Chestermiller,

Some of the numbers i gave earlier were wrong. The drum is actually 200L and measures approx 880mm high.

The drop pipe was constructed from a 3"x1" reducer welded to a length of 1" pipe. The drop pipe was inserted into the drum opening so that the bottom of the pipe rests approx 100mm above the bottom of the drum. The reducer sits above the level of the drum and allows the nozzle to be inserted. Nozzle diameter is 38mm (approx 35mm internal dia).

Drum is considered full once it reaches approx 50mm below top surface. Not sure how this is relevant though? Backflow was occurring as soon as the level of liquid in the drum reached the bottom of the drop pipe.

What’s the approximate viscosity of the fuel?

 

[Kieran989]

What’s the approximate viscosity of the fuel?

At 25degC kinematic viscosity of JET A1 is approx 1.5 mm^(2)/s and density of approx 800kg/m^3

 

[Chestermiller]

A couple of other questions:

Do you know whether the drop pipe is running full during the situation in which the lower exit is not submerged? Or is there a continuous path for air from the top to the bottom?

The reducer: Is that a converging section (like a funnel) that makes direct contact and is sealed to the top of the drop tube?

 

[Mohankpvk]

Chestermiller, please explain whether continuity equation can be applied to cases where a part of the pipe is changed.A few of my friends and a person in this forum claim that it can be applied.But earlier a few of you explained it cannot be applied.

 

[Chestermiller]

Chestermiller, please explain whether continuity equation can be applied to cases where a part of the pipe is changed.A few of my friends and a person in this forum claim that it can be applied.But earlier a few of you explained it cannot be applied.

At steady state (no parameters changing as a function of time at any given location), the product of density times velocity times flow area is constant. This is what the continuity (conservation of mass) equation tells us. If this is what you mean by the continuity equation being applied, then yes it can be applied, even to parts of a pipe where the flow area changes.

This topic has taken the discussion in this thread a bit off the track, and I would like to keep it on the track. If you have any further questions about this, please start a new thread.

 

[Kieran989]

A couple of other questions:

Do you know whether the drop pipe is running full during the situation in which the lower exit is not submerged? Or is there a continuous path for air from the top to the bottom?

The reducer: Is that a converging section (like a funnel) that makes direct contact and is sealed to the top of the drop tube?

The reducer is a standard ASME pipe fitting that was welded to the 1" pipe. It allowed us to insert the nozzle into the drop pipe.

Regarding the path of air its too hard to say. I would assume at 130L/min the 1" pipe would have been close to full of liquid if not completely full

 

[Chestermiller]

I'm going to do some "walk-through" calculations to try to get a handle on what is happening. These first calculations will focus on the case of the 1" drop pipe, where the fluid level has not risen enough to block the outlet. I'm going to assume that the pipe is running full. I want to look at the pressure variations in the pipe, and to see how the hydrostatic component compares with the viscous frictional drag component. For a fluid flow of 130 lpm, the average downward flow velocity is $$V=\frac{130000}{60\left(\frac{\pi (2.54)^2}{4}\right)}=428\ cm/s=4.28\ mps$$ The fluid density is 800 kg/m^3, so the mass flow rate is:
$$\dot{m}=\frac{130(0.8)}{60}=1.73\ kg/s$$The fluid viscosity is 0.0012 Pa.s, so the Reynolds number is:
$$Re=\frac{4\dot{m}}{\pi D \mu}=\frac{4(1.73)}{\pi(0.0254)(0.0012)}=72400$$
This makes the flow turbulent. From the Blasius equation for the fanning friction factor, we have:
$$f=\frac{0.079}{(Re)^0.25}=0.00482$$
Based on this, the viscous shear stress on the wall is: $$\tau=\frac{1}{2}\rho V^2f=(0.5)(800)(4.28)^2(0.00482)=35.2 Pa$$
The frictional pressure drop contribution in the tube would be $$\Delta P=4\frac{L}{D}\tau=4\frac{0.88}{0.0254}35.3=4892 Pa$$
The hydrostatic pressure contribution would be $$\Delta P=\rho g L = (800)(9.8)(0.88)=6899 Pa$$
Since, for the open tube, the exit pressure is 0 Pa gauge, the pressure at the top of the drop tube would be predicted from these calculations to be 4892 - 6899 = -2007 Pa = -0.3 psi. So, if the tube were running full, the pressure at the entrance to the drop tube would be a slight vacuum. This is because the weight of the fluid would be more than the ability of the viscous frictional force at the wall to support that weight. It isn't clear what is happening in the region approaching the drop tube from above that would cause this small pressure deficit. To be sure though, the frictional drag in the 1" tube at least comes somewhat close to offsetting the weight of the fluid. This would not be the case in the 3" drop pipe, where the hydrostatic contribution would not change, but the frictional component would be much smaller. This would allow the fluid to flow downward much more freely.

The effect of blockage at the bottom of the drop tube on the pressure distribution and downward flow would not be immediately obvious. It would seem that, for the 1" pipe, it could flip the situation so that the hydrostatic component is no longer sufficient to overcome the frictional drag plus the exit pressure resistance. To quantify the exit pressure resistance, it probably would help to carry out a computational fluid dynamics calculation. But I think it would be very unlikely that the resistance at the exit of the pipe would be enough to overcome the hydrostatic contribution in the 3" pipe (where frictional drag is not really playing much of a role).

 

[Sherwood Botsford]

Hmm. Something odd here. Your flow rate is about 2 l/s. That doesn't seem unreasonable for water under 3 feet of head to fall into existing pool of liquid. I'm wondering if it is an 'entraining' effect. When the bottom of the pipe is open, the air column in the pipe is at atmospheric pressure. As the opening closes, the falling liquid carries air underneath, dropping the pressure in the drop pipe, and causing the nozzle shut down. (Do they respond to a drop in back pressure as well as a rise?)

This could be tested by putting a hole, say 1/4" in the side of the top of the drop pipe.

The other possibility is some sort of hydraulic jump effect. On contact with the lip of the down pipe, flow abruptly slows, backing up the pipe. Increase in pressure trips the nozzle.

* Test: Attempt it again, but after it shuts off the first time, squeeze the nozzle slowly to establish a flow. I've had some cars do this -- you had to accelerate the fill rate slowly.

* Test: Cut the bottom of the drop pipe at a 45 degree angle. This means the transition from an air exit to a liquid exit is slowed down.

* How much time between the end of the drop pipe being immersed, and the fluid backing up and shutting off the nozzle. How does this compare to the time to fill a 1" pipe at 130 l/m?

* What happens if only the bottom 6 inches of the drop pipe are replaced with larger pipe? Or the bottom 18 inches?

* what is the result if you perforate the drop pipe, putting a line of 1/4" holes along it's length.