- #1
EastWindBreaks
- 128
- 3
Homework Statement
Hydrostatic force on a plane surface ex:
Hydrostatic force on a gate:
Homework Equations
The Attempt at a Solution
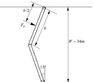
why can't we just use the formula in the red box above for problem 3.57?
instead I have to use integral
I am confused, how does this gate different from a slanted plane. if I look at the gate from front view, i feel like they are just the same thing. How does
Attachments
-
 upload_2017-11-13_3-12-35.png28.4 KB · Views: 967
upload_2017-11-13_3-12-35.png28.4 KB · Views: 967 -
 upload_2017-11-13_3-15-19.png28.1 KB · Views: 1,215
upload_2017-11-13_3-15-19.png28.1 KB · Views: 1,215 -
 upload_2017-11-13_3-17-14.png6.3 KB · Views: 537
upload_2017-11-13_3-17-14.png6.3 KB · Views: 537 -
 upload_2017-11-13_3-17-44.png15.3 KB · Views: 506
upload_2017-11-13_3-17-44.png15.3 KB · Views: 506 -
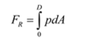 upload_2017-11-13_3-38-14.png932 bytes · Views: 453
upload_2017-11-13_3-38-14.png932 bytes · Views: 453 -
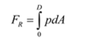 upload_2017-11-13_3-38-24.png932 bytes · Views: 460
upload_2017-11-13_3-38-24.png932 bytes · Views: 460
Last edited: