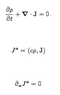Why Need Covarient Form of Electrodynamics?

[physicist 12345]

hello this is my first topic here and i hope good discussion or answer to my question

As i understand the Maxwell equation keep its form in all frames so why i need to make a covarient formulation form of electrodynamics ?

for example what the covarient form of continuity equation give me !

 

[PeterDonis]

this is my first topic here

Welcome to PF! Please note that the thread levels ("B", "I", and "A") are meant to show the level of your background knowledge in the subject matter. Based on your post, I have changed the level of this thread to "B".

the Maxwell equation keep its form in all frames

Yes, provided we transform all quantities appropriately.

why i need to make a covarient formulation form of electrodynamics ?

I assume that by "covariant formulation" you mean a formulation in terms of 4-vectors and 4-scalars instead of 3-vectors and 3-scalars. The reason this is done is that it makes it much easier to transform all quantities appropriately, and to see explicitly how the laws remain invariant under Lorentz transformations.

what the covarient form of continuity equation give me

This is easily found by looking in textbooks or online resources. It is much too broad a subject for a PF thread; once you have taken some time to build your background knowledge, you should be able to ask a more specific question.

 

[physicist 12345]

thank you very much for quick answer

my question about continuity equation not about the difference but i ask what i get from the covarient form instead of usual form (how i benefit from writing it in covarient form)

also as you say that new formulation to make work much easier then if we use the ordinary (not modified equations) we will get the same results
(i.e i use the same form of Maxwell equation in different frames )

 

[PeterDonis]

as you say that new formulation to make work much easier then if we use the ordinary (not modified equations) we will get the same results
(i.e i use the same form of Maxwell equation in different frames )

I don't understand what you mean by this. Maxwell's Equations already take the same form in different frames, whether you use 3-vectors and 3-scalars or 4-vectors and 4-scalars to express them, as long as you transform between frames using the Lorentz transformations for all quantities. That's what you were saying in the OP when you said "the Maxwell equation keep its form in all frames".

 

[physicist 12345]

I meant by two forms the equations in attached photo (i meant covarience form and usual handing form)

 

[PeterDonis]

I meant by two forms the equations in attached photo (i meant covarience form and usual handing form)

These are two forms of the continuity equation, not Maxwell's Equations. The advantage of using the 4-vector form should be obvious.

 

[physicist 12345]

then the advantage of using 4- vector is just simplifying the transformation ??

 

[Dale]

i ask what i get from the covarient form instead of usual form

You get two things. First, you get brevity. Second, by writing it in covariant form you can immediately use any coordinates you like. For instance, suppose you want to use Maxwell's equations in spherical coordinates. The covariant form allows you to immediately use the same laws as you normally would use.

 

[PeterDonis]

then the advantage of using 4- vector is just simplifying the transformation ?

And making the Lorentz invariance more explicit, because the covariant quantities are always just one symbol; in the continuity equation, you have just $J^a$ instead of having to remember that the pair $\rho, \vec{J}$ go together.

 

[physicist 12345]

You get two things. First, you get brevity. Second, by writing it in covariant form you can immediately use any coordinates you like. For instance, suppose you want to use Maxwell's equations in spherical coordinates. The covariant form allows you to immediately use the same laws as you normally would use.

then the covariant form is that which keep its form under transformation (is that which is invariant)

 

[Dale]

then the covariant form is that which keep its form under transformation

Yes, that is what covariant means in this context.

 

[physicist 12345]

And making the Lorentz invariance more explicit, because the covariant quantities are always just one symbol; in the continuity equation, you have just $J^a$ instead of having to remember that the pair $\rho, \vec{J}$ go together.

And making the Lorentz invariance more explicit, because the covariant quantities are always just one symbol; in the continuity equation, you have just $J^a$ instead of having to remember that the pair $\rho, \vec{J}$ go together.

but the density (rho) is still exist as a temporal component of the current denisty

 

[physicist 12345]

Yes, that is what covariant means in this context.

Also could i think that covariance is the generalization of electrodynamic laws in diffrent frames ?

 

[PeterDonis]

the density (rho) is still exist as a temporal component of the current denisty

If you are using the 3-vector form of the equation, there is no "temporal component of the current density", because there is no "current density" 4-vector. There is just the charge density $\rho$ and the current density 3-vector $\vec{J}$. And they just happen to get mixed up together in Lorentz transformations.

 

[physicist 12345]

If you are using the 3-vector form of the equation, there is no "temporal component of the current density", because there is no "current density" 4-vector. There is just the charge density $\rho$ and the current density 3-vector $\vec{J}$. And they just happen to get mixed up together in Lorentz transformations.

it seems that i benefit from this discussion ,, i don't want to waste your time more than that but i want to thank u for your time .. i will read more and may return to ask you again ,,, deep thanks

 

[PeterDonis]

You're welcome!