Why only odd cosine terms in this Fourier series?

[zenterix]

Homework Statement

Consider the function with period $2\pi$ given by

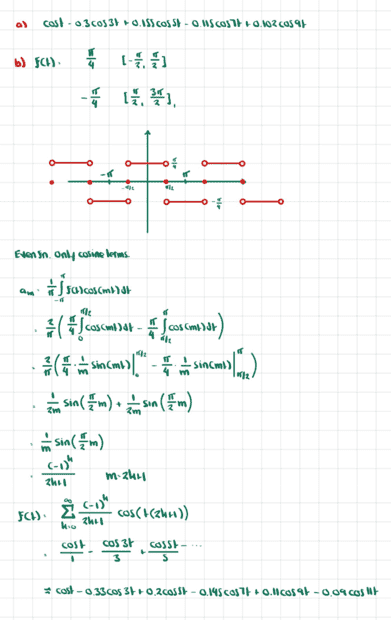
$$f(t)=\begin{cases} \frac{\pi}{4},\ \ \ \ \ t\in [-\pi/2,\pi/2] \\ -\frac{\pi}{4},\ \ \ \ \ t\in [\pi/2,3\pi/2] \\ 0, \ \ \ \ \ t=\pm\frac{\pi}{2}\end{cases}$$

Compute the Fourier coefficients for this function.

Relevant Equations

Since the function is even, there are only cosine terms in the Fourier series.

My question is what is an explanation for the fact that the Fourier series only has odd cosine terms.

This is part of a problem in a problem set in MIT OCW's 18.03 "Differential Equations" course.

This problem uses a nice online applet made for playing with Fourier coefficients.

I was able to solve everything which mainly involved finding the coefficients both by tinkering with the UI and visually arriving at them and also by computing them directly.

As we play with the UI, we quickly see that the even terms aren't useful in approximating the function with Fourier terms.

We are asked why this might be.

I am not sure why.

Below are my calculations and answers to the problems, for the record.

Part (a) are the coefficients I found by playing with the applet.

Part (b) is the calculation of the coefficients.

So of course, from the math we see that the even cosine terms disappear because of the integrals involved. But is there some kind of intuitive reason?

Note that the problem set has solutions, but they don't answer the question that I am asking here.

 

[Orodruin]

The even cosine terms are all $\pi$-periodic whereas your function is $\pi$-anti-periodic ($f(t+\pi) = -f(t)$).