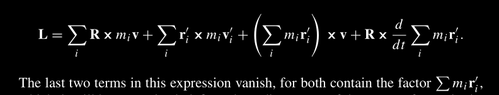Why position times mass is equal to 0 here (vanishes)?

[Istiak]

Homework Statement

Why position times mass is 0 inside Sigma summation?

Relevant Equations

F=ma

$$\sum_i m_ir_i$$

Why the term always vanishes?

There's some more equations where the mr was vanished. But, they didn't explain why it vanish. Why the term vanish? I think that's for position 0,isn't it?

 

[PeroK]

If the origin is taken as the centre of mass, then the sum is zero by definition.

 

[kuruman]

If the origin is taken as the centre of mass, then the sum is zero by definition.

I think the origin is at an arbitrary position. Vector $\vec R$ is the position of the CM of a rigid body relative to the origin. This looks like part of the proof that the angular momentum of a rigid body is the sum of the angular momentum of the CM (orbital) and about the CM (spin). The primed coordinate $\vec {r_i}'$ is the location of element $dm_i$ relative to the CM, i.e. $\vec {r_i}'=\vec r-\vec R$. Otherwise yes, the sums are zero by definition of the CM.

There's some more equations where the mr was vanished. But, they didn't explain why it vanish. Why the term vanish?

Define $\vec R$ as the position of the CM relative to an arbitrary origin and $\vec r$ and $\vec {r_i}'$ respectively as the position of $m_i$ relaitve to the origin and relative to the CM. Then $\vec r_i = \vec R+\vec {r_i}'$ so you can write the position of the CM relative to the origin, $$\vec X=\frac{\sum_i m_i\vec r_i}{\sum_i m_i}=\frac{\sum_{i} m_i(\vec R+\vec {r_i}')}{\sum{_i} m_i}=\vec R+\frac{\sum{_i} m_i\vec {r_i}'}{\sum{_i} m_i}.$$ By definition, $\vec X = \vec R$. The only way for this to be true is to have $\dfrac{\sum_i m_i\vec {r_i}'}{\sum_i m_i}=0.$