Will a sliding box fall over when it stops?

[kuruman]

Referring to #33, I followed a different route. Starting from
$\ddot\phi(\frac 13-(\mu \sin(\phi)- \cos(\phi))\cos(\phi))=(\mu \sin(\phi)- \cos(\phi))(1-{\dot\phi}^2\sin(\phi)))$ and with $\dot \phi =0$,
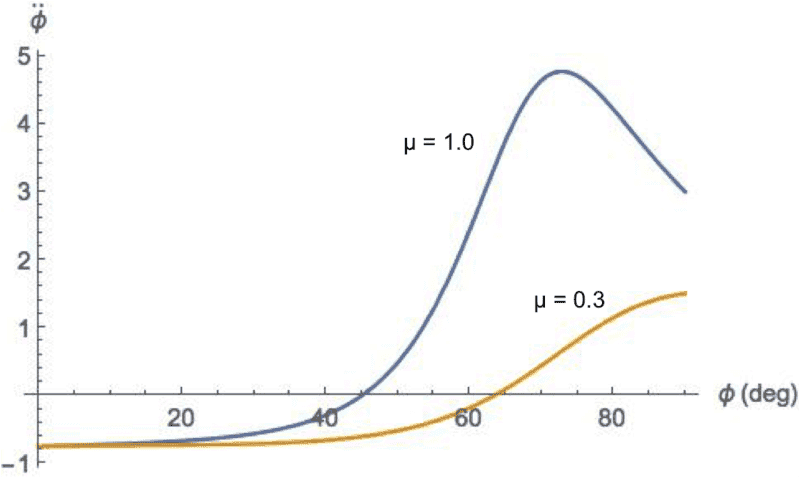
I got $\ddot\phi=\frac{\mu \sin(\phi)- \cos(\phi)}{\frac 13-(\mu \sin(\phi)- \cos(\phi))\cos(\phi)}$ which I plotted for two "typical" values of $\mu$ (see below). From the plots it is clear that the condition must be $\mu \sin(\phi) > \cos(\phi)$. Specifically, additional plots (not shown) indicate that the denominator stays positive for $\mu$ less than about 4/3 which is above what one would expect for blocks sliding on surfaces. So I think that's it.

 

[haruspex]

I plotted for two "typical" values of μ

Yes, it looks sort of reasonable for those, except why does it peak for μ=1 and φ<π/2?
And it gets really weird for larger μ. Try μ=1.6.

 

[kuruman]

I was incommunicado for several days because of hardware problems. I thought about this some more and here is what I have.

Ahem.. correcting my algebra..

For the condition for starting/continuing to tip we can take $\dot\phi=0$ and $\ddot\phi>0$.
Will also assume φ≤π/2, since the development in post 18 might be invalid else.
From the equation in post #18:
$(\frac 13-(\mu\sin(\phi)-\cos(\phi))\cos(\phi))(\mu\sin(\phi)-\cos(\phi))>0$
Writing $\mu=\tan(\alpha)$ we can break this into two cases.
1. $\mu\sin(\phi)>\cos(\phi)$ (i.e. φ+α>π/2)
$\frac 13>(\tan(\alpha)\sin(\phi)-\cos(\phi))\cos(\phi)$
$\frac 23>\tan(\alpha)\sin(2\phi)-1-\cos(2\phi)$
$\frac 53>\tan(\alpha)\sin(2\phi)-\cos(2\phi)$
$5\cos(\alpha)>3(\sin(\alpha)\sin(2\phi)-\cos(\alpha)\cos(2\phi))$
$5\cos(\alpha)+3\cos(\alpha+2\phi)>0$
Looks weird, but..
2. φ+α<π/2
As above but with all inequalities reversed. I'd say the conclusion for this case is it can't happen.

Still looks mighty strange...

Case 1 is always the case if there is to be tipping. Here is the reason. Suppose the block is just sliding with friction but not tipping, like a book sliding across a table on its cover. The torque equation about the CM is $\mu N h-Ns=0$. Here $s$ is the distance from the point vertically below the CM to the point where the $N$ acts on the block. As $\mu$ increases, $s$ must increase to compensate. However $s$ cannot increase past $w$ the half width of the base. At the threshold, $\mu N h-Nw=0$. Tipping occurs if $w$ is less that the threshold value, $w<\mu h$. Let $\phi_0$ be the angle between $A$ and the horizontal. Then $\cos(\phi_0)=w/A$ and $\sin(\phi_0)=h/A$. The tipping condition becomes $\cos(\phi_0)<\mu \sin(\phi_0)$ or $\mu \sin(\phi_0)-\cos(\phi_0)>0.$ Thus if the condition is satisfied and the block starts tipping, $\phi$ increases and $\mu \sin(\phi)-\cos(\phi)>0$ remains positive since the sine increases and the cosine decreases but remains positive for $\phi_0<\phi<\pi/2$. Now since the numerator is always positive, one has to ensure that the denominator be also positive.
$\frac 13>(\tan(\alpha)\sin(\phi)-\cos(\phi))\cos(\phi)$
$\frac 13>\frac{(\sin(\alpha)\sin(\phi)-\cos(\phi)\cos(\alpha))}{cos(\alpha)}\cos(\phi)$
$\cos(\phi+\alpha)\cos(\phi)>-\frac {\cos(\alpha)} {3}.$