Will this be the second smallest?

  • MHB
  • Thread starter evinda
  • Start date
In summary, to find the second smallest element in a tournament tree, we can compare the smallest element ($d_2$) to the smallest element of the left subtree ($d_1$). Then, we can compare that smallest element to the smallest elements of the right subtree ($a_{12}$, $b_5$, $c_4$) to determine the second smallest element.
  • #1
evinda
Gold Member
MHB
3,836
0
Hi! (Happy)

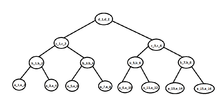
Suppose that we have this tournament tree and we want to find the second smallest element.View attachment 3840Suppose that $d_2<d_1$. Then we know that the smallest element is $d_2$.
Then we will know that the smallest element of the left subtree is $d_1$ and it suffices to find the smallest element of the right subtree in order to compare them, right?
If we suppose that $c_3=b_6=a_{11}=d_2$ then we have to compare $a_{12} $ with $b_5$, the smallest of them with $c_4$ and finally the smallest of these two elements which we considered at last with $d_1$. The smallest of them will be the second smallest element, right? (Thinking)
 

Attachments

  • tree9.png
    tree9.png
    8.4 KB · Views: 66
Technology news on Phys.org
  • #2
Yes, that's correct. The second smallest element will be the smallest of the elements you compared: the smallest of $a_{12}$, $b_5$, $c_4$, and $d_1$.
 

FAQ: Will this be the second smallest?

Will this be the second smallest number in the sequence?

The answer to this question depends on the specific sequence being referenced. In some cases, it may be the second smallest number, while in others it may not be.

Can you explain why this is the second smallest?

The designation of "second smallest" is relative and can vary depending on the context and criteria used to determine the smallest number. It may be helpful to provide more information about the sequence or comparison being made.

Is there a mathematical formula to determine the second smallest number?

There is no single formula or method for determining the second smallest number in a sequence. It will depend on the specific sequence and its properties.

Can there be more than one second smallest number?

In some cases, there may be multiple numbers that are tied for the second smallest in a sequence. This can happen if there are repeated values or if the sequence is not strictly ordered.

How can I find the second smallest number in a large dataset?

There are various algorithms and techniques that can be used to find the second smallest number in a dataset. Some examples include sorting the data and then selecting the second element, or using a divide and conquer approach. The most efficient method will depend on the size and nature of the dataset.

Similar threads

MHB Find Next Smallest & Greatest Key in BST
Replies
1
Views
1K
MHB How many comparisons are needed?
Replies
1
Views
1K
MHB Find the second smallest element
2
Replies
58
Views
8K
MHB Finding the $j^{th}$ Smallest Element in an AVL Tree
Replies
7
Views
2K
MHB Finding Depth & Height of Node w/ Key $r$ in $\text{AVL tree}$
Replies
15
Views
3K
MHB Drawing Binary Tree: Exploring Pre-Order & In-Order Traversal
Replies
14
Views
3K
MHB A decision tree has an expected depth of at least log n
Replies
1
Views
1K
MHB Which node satisfies this property?
Replies
20
Views
4K
I Optimization problem with multiple outputs: impossible?
Replies
6
Views
2K
MHB What Is the Smallest Good Number for a Subset of Squares?
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top