annamal
- 393
- 33
Will this dipole rotate or change position? The external electric field is in black. Two charges with their electric fields are drawn in orange.
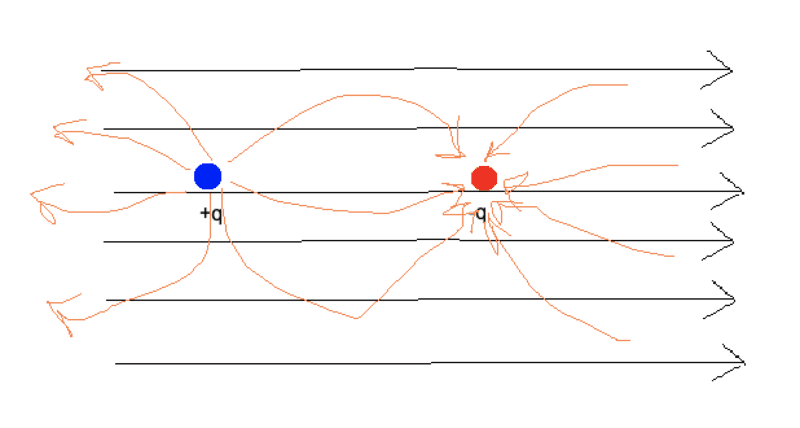
That's what @DaveE just said. And if the two charges are held rigidly at their current separation (hence, a diople), they will be rotated by those forces until they align with the field. But since the E field is constant in magnitude in the area that you show, what is the "Net" force on the two charges overall?annamal said:which means, the blue +q should be repelled and move away with the red -q moving forward.
Shouldn't it be 0 in this unstable equilibrium position?berkeman said:That's what @DaveE just said. And if the two charges are held rigidly at their current separation (hence, a diople), they will be rotated by those forces until they align with the field. But since the E field is constant in magnitude in the area that you show, what is the "Net" force on the two charges overall?
You asked about the net force. The net force should be 0.berkeman said:Shouldn't what be zero? The net force and torque? I suppose so, but it's a very unstable equilibrium as drawn, and will experience a torque fairly soon that flips it into the stable equilibrium position (after a period of oscillations that will depend on any damping that is present).
Correct, but not the net torque. You were asking about how the dipole would move in this situation.annamal said:You asked about the net force. The net force should be 0.