Wind Speed required to topple Patio Screen Support

[crazy_emu]

I want to install two retractable patio screens on my patio but there aren't any columns, so I'll need to install a post/column to attach the screens and guide rails to. My concern is making sure I install an adequate post for support during winds. If I can avoid it, I'd like to stay away from installing stringers/headers from the corner post to the sides of my home. The housing where the screens roll up are pretty stout; all extruded aluminum, and would be installed from the post to the sides of the house, more or less acting as the stringers/headers.

Initially, I was using a calc for wind load that estimates the force at F = A x P x Cd. The two screens total an area of 468sqft, the Pressure is calculated using 75mph wind and the drag coefficient used is 1.5. This gives a force of 5700 lbft. Though, this assumes all force is perpendicular to the screens and is the total area of both screens combined.

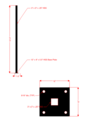
Assuming the force on the screens is accurate, what would be the force transferred to the base plate of the tube steel post, anchors and concrete? I plan to use 1/2" x 5-1/2" Hilti Kwik Bolt anchors with minimum 3.5" embedment. Any help would be appreciated. I'm unsure of how to move forward with evaluating what would be required of the post and anchors to adequately resist wind loads.

Files attached showing sketches of patio layout, corner post and profile view of the patio screens.

 

[Baluncore]

Welcome to PF.

The housing where the screens roll up are pretty stout; all extruded aluminum, and would be installed from the post to the sides of the house, more or less acting as the stringers/headers.

You need the design and installation sheet from the screen manufacturer. There will be a force bending the housings when the wind blows, due to tension in the stretched fabric being multiplied by the triangle of forces. Look for existing examples of those screens being installed in your neighbourhood.

Are the screen housings really designed to be supported at the ends only?

This is not a job for beginners.
You need a qualified engineer with an insurance policy.

I would expect dynamic wind pressure, on the screen, to peak at about 50 lb/sqft. So 468 sqft would give 23,400 lbs perpendicular. Our estimates differ. My value might be high, but your estimate might be too low for safety.

 

[crazy_emu]

Welcome to PF.


You need the design and installation sheet from the screen manufacturer. There will be a force bending the housings when the wind blows, due to tension in the stretched fabric being multiplied by the triangle of forces. Look for existing examples of those screens being installed in your neighbourhood.

Are the screen housings really designed to be supported at the ends only?

This is not a job for beginners.
You need a qualified engineer with an insurance policy.

I would expect dynamic wind pressure, on the screen, to peak at about 50 lb/sqft. So 468 sqft would give 23,400 lbs perpendicular. Our estimates differ. My value might be high, but your estimate might be too low for safety.

Baluncore,
The screens are designed to be supported on the ends and are also interlinked with the guide rails which are secured every couple feet. The housing is very stout, and not flimsy rolled form metal.

Would you show me the math on how you came up with 23,400 lbs of force? I'm certainly not positive of my number, but would like to see your process.

 

[Baluncore]

It was just a memory of the worst case normally expected during storms.

I suggest you compute dynamic pressure for the worst-case wind gust.
https://en.wikipedia.org/wiki/Dynamic_pressure
Pa = ½·m·v²
If your worst case is 75 mph, then you live in a quiet location.

75 mph = 33.528 m/sec. 33.528² = 1124.1
Air density = 1.225 kg/m3
Pa = 0.5 * 1.225 * 1124.1 = 688.5 kg/m²
688.5 Pa = 0.1 psi = 14.4 lb/ft²
14.4 * 468 sq·ft = 6,739 lbs.

100 mph = 44.704 m/sec.
0.5 * 1.225 * 1998 = 1224 Pa.
1224 Pa = 0.1775 psi = 144 * 0.1775 = 25.56 lb/ft
25.56 * 468 sq·ft = 11,962 lbs.

I ignored the drag coefficient.

 

[Baluncore]

The screens are designed to be supported on the ends and are also interlinked with the guide rails which are secured every couple feet.

I have no idea how to interpret that information without some idea of the screen installation and orientation.

 

[crazy_emu]

Thank you for showing the math on that. I'll absolutely be looking for an engineer before installing these screens (if I install them at all)!


How does the math change for the following:
We've assumed a perpendicular force from the wind, and on the entirety of the screens as though they are one screen and on the same plane. What does the math look like if we take into account a 45 degree angle of approach, rather than perpendicular? (Or any angle other than 90)

 

[Baluncore]

At any other angle, look at the profile from that direction.
45° will reduce the target width to 1/√2 = 70.71% of the total area.

Salmon E. H. Materials and Structures. 1938. Reports measurements over 50 lb/ft² on bridge plate pressure gauges. Salmon also gives the following empirical relationship.
Pressure = 0.0032 * V² lb/ft² where v is in mph .
The maximum velocity of a gust is taken as 1.3 * v + 1.5 ; where v is the average wind speed.
75 mph * 1.3 + 1.5 = 99 mph .
0.0032 * 10,000 ≈ 32 lb/ft² .

 

[crazy_emu]

At any other angle, look at the profile from that direction.
045° will reduce the target width to 1/√2 = 70.71% of the total area.

Salmon E. H. Materials and Structures. 1938. Reports measurements over 50 lb/ft² on bridge plate pressure gauges. Salmon also gives the following empirical relationship.
Pressure = 0.0032 * V² lb/ft² where v is in mph .
The maximum velocity of a gust is taken as 1.3 * v + 1.5 ; where v is the average wind speed.
75 mph * 1.3 + 1.5 = 99 mph .
0.0032 * 10,000 ≈ 32 lb/ft² .

How would these forces be applied to the base of the post and anchors to determine the force needed for the post/base/anchors to fail?

 

[RMW]

It would be very un-pleasant to be sitting on your patio in winds anywhere near that speed. When a storm is imminent just roll up the screens, go indoors and pour yourself a double Scotch.

 

[crazy_emu]

It would be very un-pleasant to be sitting on your patio in winds anywhere near that speed. When a storm is imminent just roll up the screens, go indoors and pour yourself a double Scotch.

Couldn't agree more!

 

[Joe591]

Baluncore,
The screens are designed to be supported on the ends and are also interlinked with the guide rails which are secured every couple feet. The housing is very stout, and not flimsy rolled form metal.

Would you show me the math on how you came up with 23,400 lbs of force? I'm certainly not positive of my number, but would like to see your process.

for this one tank we built the consulting engineer legitamately used 200km/h in his calculation for wind resistance. the chances of such a wind is quite low.