Work and energy- 1 stationary and 1 swinging block (table+pulley)

[natasha13100]

Homework Statement

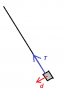
A box of mass M is at rest on a horizontal table. The coefficient of static friction between the box and the table is k. The box is connected by a taut string to a block of unknown mass m, initially held horizontally as shown and then released. The box begins to slide at the instant the block reaches the bottom point of its swing. (See attached figure.) Find the mass m of the block.

Homework Equations

F_f=kN
G=mg (g=9.8)
most likely work and energy equations such as K=kinetic energy=1/2mv₂, U_g=potential energy due to gravity=mgh, W=work=∫Fdr, U=prtential energy=-∫Fdr, etc.

The Attempt at a Solution

I need help understanding where I went wrong and how to complete this problem using work and energy considerations.
F_f=kN
N=-G_M and G_M=Mg so F_f=kMg
The block begins to move when the force of friction is overcome so T=tension in string=kMg.
This is where I start getting lost. I did T=G_m=mg so kMg=mg and m=kM.

 

[TSny]

This is where I start getting lost. I did T=G_m=mg so kMg=mg and m=kM.

Hello.
If m were just hanging at rest, then T would equal mg. But, it's swinging in circular motion.

 

[natasha13100]

Hello.
If m were just hanging at rest, then T would equal mg. But, it's swinging in circular motion.

So if I understand correctly, now I have to find the circular motion up until the bottom point of the swing. At this point, energy and not force will be important so I will have to find velocity. I am not sure how to do this because the only thing we ever covered with circular motion was uniform circular motion and I don't think that applies here due to gravity. (or does it?)

 

[TSny]

At the bottom of the swing, there will not be any horizontal forces acting on m. So, it's speed will essentially be constant in the neighborhood of the bottom of the swing. So, you can apply what you know about uniform circular motion at that point.

But, you will need to find an expression for the speed of m when it arrives at the bottom. Maybe you can use energy ideas to relate the speed of m at the point of release to the speed when it arrives at the bottom of its swing.

 

[natasha13100]

At the bottom of the swing, there will not be any horizontal forces acting on m. So, it's speed will essentially be constant in the neighborhood of the bottom of the swing. So, you can apply what you know about uniform circular motion at that point.

But, you will need to find an expression for the speed of m when it arrives at the bottom. Maybe you can use energy ideas to relate the speed of m at the point of release to the speed when it arrives at the bottom of its swing.

Well I got partial credit for attempting the problem in a reasonable manner, but I still don't understand the concept. Could you please give me an explanation of how this works? General formulas or specifics would be greatly appreciated. This is really bothering me. I set up an equation relating the kinetic energy to the work and potential energy. However, I keep getting an equation involving the length of the string which is unknown. Could anyone please explain it so I can understand. (I'm just in an introductory physics class and this is a challenge problem.)

 

[TSny]

Using energy, what do you get for the speed of the mass at the bottom of the swing? Don't worry if v depends on the length of the string L. Maybe L will cancel later.

 

[natasha13100]

Using energy, what do you get for the speed of the mass at the bottom of the swing? Don't worry if v depends on the length of the string L. Maybe L will cancel later.

1/2mv2=mgL+mg/cos(θ) if θ is the angle between the string and the vertical.
v=√(g/2*(L+1/cos(θ))

 

[TSny]

1/2mv²=mgL+mg/cos(θ) if θ is the angle between the string and the vertical.
v=√(g/2*(L+1/cos(θ))

You can tell something's wrong with this equation since L and 1/cos(θ) do not have the same units. (Terms can only be added if they have the same units.)

Conservation of energy implies that the energy of the block at the moment it reaches the bottom of its swing is the same as the energy of the block at the moment it is released at the top.

E_bottom = E_top.

How would you express each side of this equation?

 

[natasha13100]

You can tell something's wrong with this equation since L and 1/cos(θ) do not have the same units. (Terms can only be added if they have the same units.)

Conservation of energy implies that the energy of the block at the moment it reaches the bottom of its swing is the same as the energy of the block at the moment it is released at the top.

E_bottom = E_top.

How would you express each side of this equation?

I redid the equation, but without having worked out the exact expression for work. I know work is Fx but the force is throwing me off. I also know for varying force, w=∫x_i→x_f(F(x)dx)
1/2mv2=mgL+Fx F is the force acting on the string and x is the distance the string travels.
v=√(gL/2+Fx/(2m))
well E=U since the block of mass m is not moving at the top when it is released so 1/2mv²=mgL

 

[TSny]

I redid the equation, but without having worked out the exact expression for work. I know work is Fx but the force is throwing me off. I also know for varying force, w=∫x_i→x_f(F(x)dx)
1/2mv2=mgL+Fx F is the force acting on the string and x is the distance the string travels.
v=√(gL/2+Fx/(2m))

The force of the string on the block always acts perpendicularly to the direction the block is traveling. (We usually refer to the force of the string as the "tension" of the string.) In the picture, I have represented the tension by T and d represents a little distance that the block will move during a short time. You can see that T and d are perpendicular. How much work does T do on the block as the block moves the distance d? Can you see what the total amount of work will be by the tension force on the block as it swings all the way down?

well E=U since the block of mass m is not moving at the top when it is released so 1/2mv²=mgL

If you were able to see that the work done by the tension force is zero, then you end up with 1/2mv²=mgL, as you stated! Good. So, what do you get when you solve for the speed v of the block at the bottom of the swing?

 

[natasha13100]

So, what do you get when you solve for the speed v of the block at the bottom of the swing?

v=√(2gL)

 

[TSny]

v=√(2gL)

Yes. You can see that you next need to find the tension at the bottom of the swing, because it's the tension force that will start the box sliding. Can you see how to get the tension? Hint: it's a force, so use a basic law involving forces and apply the law to the block at the moment it reaches the bottom of its swing.

 

[natasha13100]

Can you see how to get the tension?

In order for the block to start moving,
μ_sMg=mg+T so T=μ_sMg-mg

 

[TSny]

In order for the block to start moving,
μ_sMg=mg+T

What's the reasoning behind that?

 

[natasha13100]

Actually at the bottom of the swing, F=mv²/L due to uniform circular motion so T=m*2g

 

[natasha13100]

T must also be equal to kMg so that tension can overcome static friction. Therefore, m=kMg/2. Is that correct?
I trying to combine too much at once and got confused which is how I got the equation in post 13.
I thought that in order for friction to be overcome, T+mg=f=kN=kMg so T=kMg-mg

 

[TSny]

Actually at the bottom of the swing, F=mv²/L so T=m*2g

Newton's second law says F_net = ma or ƩF = ma. For circular motion, it's the sum of all forces acting toward the center that equals mv²/r.

 

[TSny]

T must also be equal to kMg so that tension can overcome static friction.

Yes, where k is the coefficient of friction.

Therefore, m=kMg/2. Is that correct?

No, but once you get the correct tension I think you will have it.

 

[natasha13100]

Newton's second law says F_net = ma or ƩF = ma. For circular motion, it's the sum of all forces acting toward the center that equals mv²/r.

Ok so T+mg=mv²/r. That means that T=m*2*g*L/L-mg=2mg-mg=mg

 

[TSny]

Ok so T+mg=mv²/r. That means that T=m*2*g*L/L-mg=2mg-mg=mg

Not quite, but close! Do the forces T and mg act in the same direction on m?

 

[natasha13100]

Not quite, but close! Do the forces T and mg act in the same direction on m?

No they do not. T=m*2*g*L/L+mg=2mg+mg=3mg.
kMg=3mg
m=kM/3
Is that it? I think it is because that is what the answer was, but I just want to make sure.
Thank you so much! You are amazing. I feel like I had so many misconceptions and you cleared them all up. :)

 

[TSny]

m=kM/3
Is that it?

I believe it is. Good work.