Work and Energy for a mass sliding down a curved ramp (why does the ramp move?)

[MatinSAR]

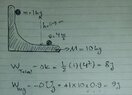
Homework Statement

An object descends from the rest state from above the surface and goes to the right And the surface goes to the left due to the object coming down(Friction between object and surface and friction between the surface and ground are both zero). What force causes the surface to move to the left? 1 joule of negative work is done by what force?

Relevant Equations

W=K2-K1

What force causes the surface to move to the left?
Can I say that it's due to the force component of the weight along the vertical force of the surface?

 

[Lnewqban]

What force causes the object to move to the right?

 

[MatinSAR]

What force causes the object to move to the right?

It's weight.

 

[PeroK]

Could gravity have a horizontal component?

 

[Lnewqban]

It's weight.

But not the whole weight.
Only its horizontal component at each instant.

The vertical component of the weight force only pushes down in the direction in which there is no freedom of movement.

Conservation of momentum dictates how much each mass moves in opposite directions.

Note that those are internal forces to the 2-mass system.
There is no external force making the combined center of mass of the whole system relocate from its original position.

 

[jbriggs444]

What force causes the surface to move to the left?
Can I say that it's due to the force component of the weight along the vertical force of the surface?

You can choose to split the gravitational force into a component normal to the surface and a component tangential to the surface. That much is fine.

However, the gravitational force still acts on the ball alone, not on the surface. Newton's second law still applies. The force of gravity on the ball in the direction perpendicular to the surface is not necessarily equal to the normal force of the ball on the surface.

 

[MatinSAR]

Could gravity have a horizontal component?

I made a mistake. I will correct: The force that the body exerts on the surface due to its weight has two components: perpendicular to the surface and parallel to the surface. Does this vertical component cause the surface to go to the left?!

Only its horizontal component at each instant.

So is it true to say this vertical component cause the surface to go to the left?!

However, the gravitational force still acts on the ball alone, not on the surface. Newton's second law still applies. The force of gravity on the ball in the direction perpendicular to the surface is not necessarily equal to the normal force of the ball on the surface.

Thank you. So Does the force of gravity on the ball in the direction perpendicular to the surface cause the surface to move to the left?!
And ...

What about the force that hase done -1J work ?! Does the component perpendicular to the surface of the force of weight do the work?

 

[jbriggs444]

So Does the force of gravity on the ball in the direction perpendicular to the surface cause the surface to move to the left?!

The force of gravity on the ball acts on the ball. It does not act on the surface.

Forces are not transitive.

 

[MatinSAR]

The force of gravity on the ball acts on the ball. It does not act on the surface.

Forces are not transitive.

I don't know why I have repeated my mistake ... sorry ...

The force that the body exerts on the surface due to its weight has two components: perpendicular to the surface and parallel to the surface. Does this vertical component cause the surface to go to the left?!

 

[jbriggs444]

I don't know why I have repeated my mistake ... sorry ...

The force that the body exerts on the surface due to its weight has two components: perpendicular to the surface and parallel to the surface. Does this vertical component cause the surface to go to the left?!

I think that you meant to say that the normal force of ball on surface can be regarded as having a vertical component and a horizontal component.

The vertical component acts vertically. It does not cause the surface to accelerate to the left. It would cause the surface to accelerate down into the table below. The table below prevents this acceleration.

The horizontal component acts horizontally. It does cause the surface to accelerate to the left.

 

[MatinSAR]

I think that you meant to say that the normal force of ball on surface can be regarded as having a vertical component and a horizontal component.

The vertical component acts vertically. It does not cause the surface to accelerate to the left. It would cause the surface to accelerate down into the table below. The table below prevents this acceleration.

The horizontal component acts horizontally. It does cause the surface to accelerate to the left.

The red vector causes accelerate to left , isn't it ?!
Should we check the vertical force from the body to the surface? Bullet weight force is not necessary?

 

[PeroK]

Perhaps sometimes three components are better than two!

 

[MatinSAR]

Perhaps sometimes three components are better than two!

What should the third component be?! Doesn't this assumption make the problem more difficult?

 

[jbriggs444]

The red vector causes accelerate to left , isn't it ?!

Yes.

Should we check the vertical force from the body to the surface? Bullet weight force is not necessary?

The vertical force from body on surface will not result in any vertical motion of the surface. It is constrained not to move vertically. So we can be sure that the work done by the vertical component of the normal force of ball on surface will be zero.

All this mucking about with components seems to be overcomplicating the problem. We can draw boundaries around a system of interest containing ball and surface. We can see that no energy is lost at the interface between ball and surface. It is an internal interface, so we know that no momentum change results either.
We can see that no energy is lost at the interface between surface and table and no [horizontal] momentum change either. We can see that work is done by gravity on ball. We write down equations for conservation of [horizontal] momentum and for conservation of energy, accounting for the work by gravity. We solve.

 

[MatinSAR]

But not the whole weight.
Only its horizontal component at each instant.

Thanks a lot for your help ...

Perhaps sometimes three components are better than two!

Thanks a lot for your help ...

The vertical force from body on surface will not result in any vertical motion of the surface. It is constrained not to move vertically. So we can be sure that the work done by the vertical component of the normal force of ball on surface will be zero.

Thanks a lot for your detailed answer ... wish you a good day

 

[kuruman]

And here is how the weight provides the accelerating force.
(A) The weight (blue arrow) is straight down.
(B) The blue weight is resolved into two red components, one perpendicular to the surface and one parallel to the surface.
(C) The red perpendicular component is further resolved into two black components, one horizontal and one vertical.
(D) The original single blue vector representing the weight is the same as the sum of three vectors: one down the incline, one vertical and one horizontal. The horizontal component accelerates the incline; the vertical component is cancelled by the normal force exerted by the surface; the down the incline component accelerates the block.

Disclaimer: This is not a free body diagram of the block. I omitted the normal force exerted by the incline on the block for clarity.

 

[MatinSAR]

And here is how the weight provides the accelerating force.

I have tried to do something like this this but I failed ...
Great idea !

Thank you

 

[kuruman]

By the way, the solution you posted in the photo, post #1, is incorrect. You omitted the kinetic energy of the sliding ramp that has mass 10 kg. What do you need to do to find how fast the ramp is moving when the block reaches the bottom and is moving horizontally?

 

[MatinSAR]

By the way, the solution you posted in the photo, post #1, is incorrect. You omitted the kinetic energy of the sliding ramp that has mass 10 kg. What do you need to do to find how fast the ramp is moving when the block reaches the bottom and is moving horizontally?

First, we find the total work done on the object. (Total Work is 8j)
Then we calculate the work of each force on the object.
Two forces act on the object :
1) Gravitional force : W = mgh = 9j
2) We know that there is a horizontal force that the object applies to the surface and causes it to accelerate to the left. According to Newton's third law, the surface exerts an equal amount of force on this object in the right direction, but since the force is opposite to the displacement direction, the work of this force is negative.
So work of this force is -1j ... ( Reason : W_mg + W₂ = W_T )

I think this is the reason for that negative work ...

I think that the object also does the same amount of work on the surface, but since the direction is the same, the work is positive and the total work done on the surface should be 1j ...

K₂ - K₁ = 0.5(mv^2) => 2=10v^2 => v= 0.447 m/s

 

[jbriggs444]

According to Newton's third law, the surface exerts an equal amount of force on this object in the right direction, but since the force is opposite to the displacement direction, the work of this force is negative.

There is a stronger conclusion that Newton's third law allows you to make.

1. The force of surface on ball and of ball on surface are equal and opposite by Newton's third law.
2. The interface between the two is frictionless. So the direction of the contact force between the two is normal to the surface.
3. The mating surfaces share the same velocity component in the direction of this normal force.
4. It follows that the work done by the ball on surface and by surface on ball are equal and opposite!
5. The net work done on the surface+ball system by the internal force pair between surface and ball is zero.

So we need not concern ourselves with the magnitude of the normal force. This is a good thing since it will be hard to calculate and will vary over time depending on the shape of the surface.

[We hope that the surface will be concave so that the ball does not jump clear of the curved surface, violating our naive assumptions about elasticity and that lack of relative motion in the normal direction]

 

[erobz]

First, we find the total work done on the object. (Total Work is 8j)
Then we calculate the work of each force on the object.
Two forces act on the object :
1) Gravitional force : W = mgh = 9j
2) We know that there is a horizontal force that the object applies to the surface and causes it to accelerate to the left. According to Newton's third law, the surface exerts an equal amount of force on this object in the right direction, but since the force is opposite to the displacement direction, the work of this force is negative.
So work of this force is -1j ... ( Reason : W_mg + W₂ = W_T )

I think this is the reason for that negative work ...

I think that the object also does the same amount of work on the surface, but since the direction is the same, the work is positive and the total work done on the surface should be 1j ...

K₂ - K₁ = 0.5(mv^2) => 2=10v^2 => v= 0.447 m/s

You need to think of two (distinct) conserved quantities. One of them is the total potential energy before = total kinetic energy after. The other conserved quantity will be apparent when you consider that the net external force on the system is 0, leading to another well-known conservative law. You will apply both of these results simultaneously.

 

[MatinSAR]

There is a stronger conclusion that Newton's third law allows you to make.

Thank you ... Do you think my reason for that negative work is right ?!

another well-known conservative law

Thank you ... Do you mean "conservation of linear momentum"?

 

[erobz]

Thank you ... Do you mean "conservation of linear momentum"?

Yepp

 

[MatinSAR]

Hello again ...
I have answered to the teacher but that force which hase done -1j work wasn't that horizontal component of the normal force of ball on surface. Is my teacher wrong ?!

That component acts on surface to move it leftside ...

Yepp

So the surface's speed should be 0.4 m/s ... right ?!

 

[kuruman]

Hello again ...
I have answered to the teacher but that force which hase done -1j work wasn't that horizontal component of the normal force of ball on surface. Is my teacher wrong ?!

There is no force that did -1 J work. You found that number by incorrectly applying mechanical energy conservation. Please post your revised work in which you conserve energy and momentum together.

 

[MatinSAR]

There is no force that did -1 J work. You found that number by incorrectly applying mechanical energy conservation. Please post your revised work in which you conserve energy and momentum together.

So far, I have not applied these 2 laws of consistency at the same time. The book only mentions the conservation of linear momentum and kinetic energy. Can you explain about this work or introduce a reference for reading a day when you have enough time?

I know about these formulas but here there is no potential energy ...

 

[kuruman]

So far, I have not applied these 2 laws of consistency at the same time. The book only mentions the conservation of linear momentum and kinetic energy. Can you explain about this work or introduce a reference for reading a day when you have enough time?

View attachment 317661
I know about these formulas but here there is no potential energy ...

Right. If there is potential energy to consider, then the conserved quantity is mechanical energy which is the sum of kinetic and potential energy of the two-mass system. In other words, the sum of the kinetic energies of the masses plus the potential energy when the mass is at some point on the ramp does not change as the mass descends and the ramp moves to the left.

 

[TSny]

I have answered to the teacher but that force which hase done -1j work wasn't that horizontal component of the normal force of ball on surface. Is my teacher wrong ?!

No. The teacher is not wrong.

Hint: You have calculated the net work done on the ball in the first post as well as the work done by the gravitational force acting on the ball. What other force does work on the ball?

 

[MatinSAR]

What other force does work on the ball?

Thank you ...
I only know the horizontal force that the surface exerts on the object. Reaction of the force that has been specified with red vector.

But apparently this force is not intended.

Right. If there is potential energy to consider, then the conserved quantity is mechanical energy which is the sum of kinetic and potential energy of the two-mass system. In other words, the sum of the kinetic energies of the masses plus the potential energy when the mass is at some point on the ramp does not change as the mass descends and the ramp moves to the left.

Thank you ...
Do you mean that there is no force and that -1J appeared because of my mistake in using the conservation of energy formula ?!

 

[TSny]

Thank you ...
I only know the horizontal force that the surface exerts on the object. Reaction of the force that has been specified with red vector.
View attachment 317674
But apparently this force is not intended.

Concentrate on the ball rather than the ramp. What are the individual forces acting on the ball?

You calculated the net work done on the ball in your first post. This net work on the ball must equal the sum of the works done by the individual forces acting on the ball.