MP1021
- 2
- 0
- TL;DR Summary
- Why does the charge distribution on an irregualry shaped conductor not result in different work done depending on where an attracted test charge ends up?
I am trying to wrap my head around something and would be grateful for some insight. Specifically, why the different electric fields along different paths to different areas of an irregularly shaped conductor don't impart different energies to inflowing particles.
Say we have a negatively biased conductor with regions of lower and higher surface curvature, so that the electric field will be more intense near sharper (protruding) points as compared to flatter regions of the conductor. A nearby postive test charge, starting from a region identified as at zero electric potential, and with no initial kinetic energy, will be accelerated towards the conductor and will ultimately strike it with an energy entirely determined by the potential of the conductor (and the test particle's charge), yes?
I get why, the electric force being conservative, the path taken to the same point on the conductor won't affect the test charge's final energy, but I can't make sense of why the impacting location won't affect it (just the conductor's potential). It makes sense if I think of it like gravitational potential energy- this being equivalent to two masses reaching the same final speed after travelling the same vertical distances on different slopes if there were no friction or air resistance. But when I think of it from the perspective of the charge distribution, it seems like the charge coming in from the right on the picture below should be more strongly attracted at all times along its path (as compared the particle on the left) and ultimately be moving faster before the impact.
Do I understand the situation correctly? Thanks for taking the time to read this :)
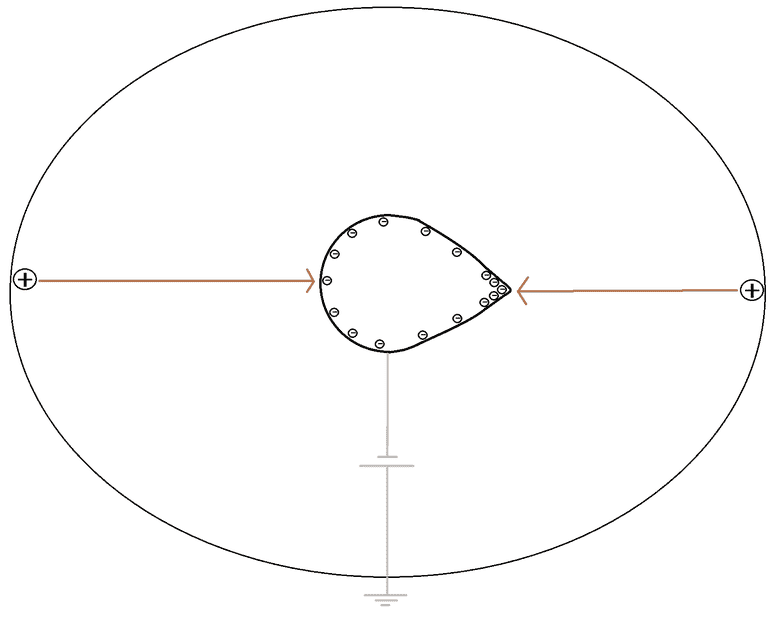
Say we have a negatively biased conductor with regions of lower and higher surface curvature, so that the electric field will be more intense near sharper (protruding) points as compared to flatter regions of the conductor. A nearby postive test charge, starting from a region identified as at zero electric potential, and with no initial kinetic energy, will be accelerated towards the conductor and will ultimately strike it with an energy entirely determined by the potential of the conductor (and the test particle's charge), yes?
I get why, the electric force being conservative, the path taken to the same point on the conductor won't affect the test charge's final energy, but I can't make sense of why the impacting location won't affect it (just the conductor's potential). It makes sense if I think of it like gravitational potential energy- this being equivalent to two masses reaching the same final speed after travelling the same vertical distances on different slopes if there were no friction or air resistance. But when I think of it from the perspective of the charge distribution, it seems like the charge coming in from the right on the picture below should be more strongly attracted at all times along its path (as compared the particle on the left) and ultimately be moving faster before the impact.
Do I understand the situation correctly? Thanks for taking the time to read this :)