- #1
I_Try_Math
- 112
- 22
- Homework Statement
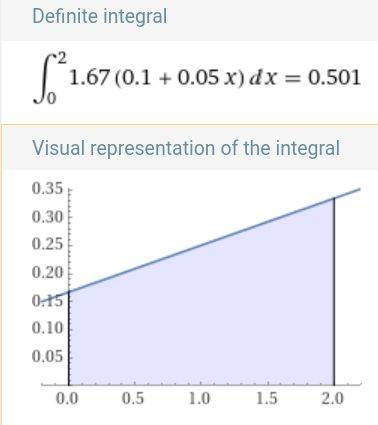
- A hockey puck of mass 0.17 kg is shot across a rough floor with the roughness different at different places, which can be described by a position-dependent coefficient of kinetic friction. For a puck moving along the x-axis, the coefficient of kinetic friction is the following function of x, where x is in m: u(x) = 0.1 + 0.05x. Find the work done by the kinetic frictional force on the hockey puck when it has moved from x = 0 to x = 2
- Relevant Equations
- [math]W = \int_0^2 F(x) \, dx[/math]
The answer key claims the answer is -0.9 J.
By my math it should be -0.501 J, is that incorrect?
By my math it should be -0.501 J, is that incorrect?