- #1
betelgeuse91
- 32
- 0
I am stuck on like the first page of thermal physics. It seems like the signs of the work done on the system are opposite when the volume is expanded and compressed. But when I imagine myself pushing or pulling the piston, I get confused from [tex]W = \textbf{F}\cdot \textbf{d}[/tex]
This work will be positive as the direction of the force and the direction of the displacement of the piston will be the same regardless of the change in volume.
What am I missing?
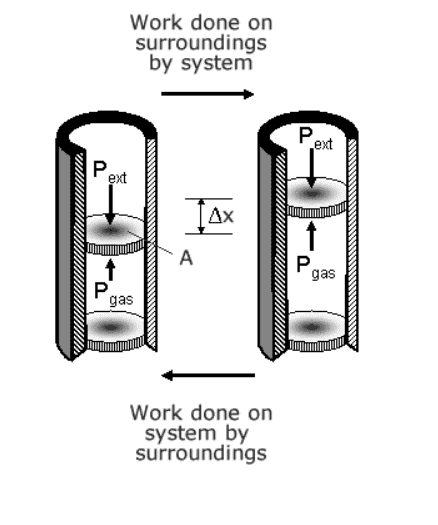
(I got the image from http://www.splung.com/content/sid/6/page/work)
This work will be positive as the direction of the force and the direction of the displacement of the piston will be the same regardless of the change in volume.
What am I missing?
(I got the image from http://www.splung.com/content/sid/6/page/work)