Shah 72
MHB
- 274
- 0
A golf ball of mass 45.9g is hit from a tee with speed 50 m/ s. The ball lands in a pond 5m lower than the tee. When the ball lands in the pond it has traveled a curved path of length 160m. The resistance acting on the ball has magnitude 0.3N
a) Find the speed of the ball just before it hits the water
I got the ans 22.5m/ s
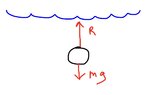
The water immediately absorbs 8J of energy from the ball. The ball then sinks vertically downwards to reach the bottom of the pond. The resistance acting on the ball had magnitude 3N and the ball just comes to rest as it reaches the bottom of the pond.
b) find the depth of the pond
I get the ans as 1. 22m . The ans in the textbook is 1.44m
Pls help
a) Find the speed of the ball just before it hits the water
I got the ans 22.5m/ s
The water immediately absorbs 8J of energy from the ball. The ball then sinks vertically downwards to reach the bottom of the pond. The resistance acting on the ball had magnitude 3N and the ball just comes to rest as it reaches the bottom of the pond.
b) find the depth of the pond
I get the ans as 1. 22m . The ans in the textbook is 1.44m
Pls help