I Work - Energy Principle Application to Fluid Flow

[Dario56]

Work - energy principle states that work done by net force acting on the body equals change in kinetic energy of the body. We are talking about continuum mechanics. This principle is usually introduced in mechanics of solid bodies. For us to describe the motion of the body, it is enough to know how center of mass of the body moves in time and space. For example, we can conclude that body accelerates, if its center of mass has different velocity in two points in time.

I am not sure how to adequately apply this principle to fluids for reasons I'll explain.

Consider fluid flowing in a pipe like in a scheme.

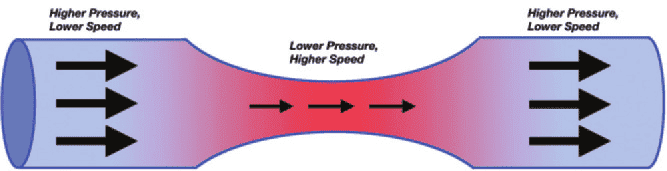
When fluid starts entering narrower section of the pipe, it accelerates. Newton's 2nd law states that in that case resultant force must act on the fluid. We can see that this force originates from difference in pressure of surrounding fluid or pressure gradient. If we take some volume of fluid between two cross sections of non - equal area in narrowing region of the pipe (control volume), we can draw free body diagram to show all forces acting on that control volume.

Doing so comes with a problem because fluid doesn't move like solid body, it flows. Concept of drawing all forces acting on control volume seems to have no sense in fluids because control volume doesn't move in space and time like solid body does. It's center of mass doesn't move in space and time like in solid bodies, but rather fluid has different velocity on different cross sections or points in the pipe.

If this is true, how should we apply Newton's 2nd law or work - energy principle to fluids? On what fluid element or control volume should we draw force diagrams and apply Newton's 2nd law? I am thinking we should probably take some differential volume element and if we want to know how much its velocity changes between two cross - sections (for inviscid fluid), we would need to calculate line integral of pressure gradient along the streamline or fluid element path. Usually, pressure gradient is constant, so line integral is equal to pressure gradient times distance between two cross - sections.

What is strange to me is that Bernoulli's equation/principle is commonly derived by work - energy principle where force diagrams are drawn for some fluid volume of finite size. This derivation seems wrong to me given what I said above and force balance in fluids can only be done for differential volume elements on particular streamline. Do you agree?

What are your thoughts?

 

[russ_watters]

If this is true, how should we apply Newton's 2nd law or work - energy principle to fluids? On what fluid element or control volume should we draw force diagrams and apply Newton's 2nd law?

You can indeed just pick a fluid element to analyze. You can Google "bernoulli's principle fluid element" and find a lot of example explanations.

 

[Dario56]

You can indeed just pick a fluid element to analyze. You can Google "bernoulli's principle fluid element" and find a lot of example explanations.

Yes, but when doing force balance, it only has sense to me that fluid element needs to be of differential volume on particular streamline given everything I said. As far as I understand, it is incorrect to do force balance on volume element of finite size while this is done in most common Bernoulli equation derivations via work energy principle, not in more advanced once in most fluid mechanics textbooks.

 

[Dale]

You can do force balance on an arbitrary volume element. The issue is that when you are using Newton's 2nd law you are analyzing a piece of matter (which can be a fluid), you are not analyzing a control volume. You can do a control volume analysis, but then you need to account for the mass flow and you are probably not going to use Newton's laws in their standard form.

 

[Dario56]

You can do force balance on an arbitrary volume element. The issue is that when you are using Newton's 2nd law you are analyzing a piece of matter (which can be a fluid), you are not analyzing a control volume. You can do a control volume analysis, but then you need to account for the mass flow and you are probably not going to use Newton's laws in their standard form.

Yes, control volume isn't a good term I used. I meant any fluid volume on which we do force balance.

If we take fluid element of some arbitrary size, do force balance and apply Newton's 2nd law, we can track how center of mass of that fluid element moves in time and space or we can determine equations of motions for center of mass, not how does fluid velocity field vary in space, from cross section to cross section. Only if fluid element has differential volume we can track how it moves in space from cross section to cross section. This is what I don't understand.

 

[Dale]

Only if fluid element has differential volume we can track how it moves in space from cross section to cross section. This is what I don't understand.

Yes, this is what is done. Typically you start with a volume of some convenient shape of arbitrary size. Then you take the limit as that size becomes infinitesimal.

 

[Dario56]

Yes, this is what is done. Typically you start with some convenient shape of arbitrary size. Then you take the limit as that size becomes infinitesimal.

Yes, I actually have no problem with this approach, which can be found in most fluid mechanics textbooks.

However, many derivations of Bernoulli's equation use work - energy principle and apply force balance for fluid element of finite size (wikipedia for example) and just leave it like that (without taking the limit as you said) which I think isn't correct and can create confusion (like it did for me) since such equation would give us equations of motion for center of mass of that fluid volume element not how velocity field changes in space and time if flow is non - stationary.

 

[russ_watters]

...such equation would give us equations of motion for center of mass of that fluid volume element not how velocity field changes in space and time if flow is non - stationary.

I'm not seeing this. If you're tracking the center of mass and ignoring the shape of the volume, you're tracking the velocity changes. And many of the online treatments I see (I don't have a textbook handy) even use fluid elements that fill a pipe/tube fully and track how it changes shape(length). That's OK in uniform flow. You track it at points (surfaces) along the path.

 

[Dario56]

I'm not seeing this. If you're tracking the center of mass and ignoring the shape of the volume, you're tracking the velocity changes. And many of the online treatments I see (I don't have a textbook handy) even use fluid elements that fill a pipe/tube fully and track how it changes shape(length). That's OK in uniform flow. You track it at points (surfaces) along the path.

I agree with you. It isn't correct that you can't trace how velocity field changes in space and time, but rather that you need to track how center of mass of chosen element moves which isn't too convenient as we firstly need to identify where it is. Taking differential volume element doesn't have this problem.

 

[Dale]

many derivations of Bernoulli's equation use work - energy principle and apply force balance for fluid element of finite size (wikipedia for example) and just leave it like that

Can you link to such an example?

 

[Dario56]

Can you link to such an example?

https://en.m.wikipedia.org/wiki/Ber... form of Bernoulli's,p and dynamic pressure q.
Section: Derivations of equation

- the same youtube video derivation

 

[Dale]

https://en.m.wikipedia.org/wiki/Ber... form of Bernoulli's,p and dynamic pressure q.
Section: Derivations of equation

- the same youtube video derivation

That one uses a differential element of volume $A \ dx$

 

[Dario56]

That one uses a differential element of volume $A \ dx$

Yes, this volume can be differential, but that is different derivation and diffierential fluid volume from what we talked about and what I think holds since in this derivation pressure forces are again looked to act on system/fluid volume between two cross sections. It is important that force balance is made on differential fluid volume on the streamline (in my opinion).

 

[Dale]

Yes, this volume can be differential, but that is different derivation and diffierential fluid volume from what we talked about

Ok, so if this example is different from what you talked about then can you please post a concrete example of a derivation that actually shows the problem you are talking about.

Or if I misunderstood, please specify exactly what you believe is amiss with this derivation. So far the only concrete objection I have heard from you was about derivations that did not use a differential parcel of fluid, and this derivation doesn’t fit that category.

 

[russ_watters]

...you need to track how center of mass of chosen element moves which isn't too convenient as we firstly need to identify where it is. Taking differential volume element doesn't have this problem.

The question in the OP was mainly about understanding the difference between a "control volume" and a "fluid element". That was answered. I'm also not clear what the remaining problem/question is.

In the NASA link, a common presentation, the fluid element is the entire cross sectional area and dx length. Since you have uniform flow you know all flow characteristics are the same everywhere on the surface. There's no ambiguity about where the center of mass is, and it doesn't really even matter as long as it's on the cross section. I don't see the inconvenience.

 

[Dario56]

Ok, so if this example is different from what you talked about then can you please post a concrete example of a derivation that actually shows the problem you are talking about.

Or if I misunderstood, please specify exactly what you believe is amiss with this derivation. So far the only concrete objection I have heard from you was about derivations that did not use a differential parcel of fluid, and this derivation doesn’t fit that category.

That derivation is what I think is not correct. Problem is that force balance should be written on differential volume fluid which IS NOT a case in this derivation.

Pressure forces on two cross sections act on system or volume element which doesn't have differential volume. What you mentioned about differential volume $Adx$ which flows through any cross section in time $dt$ is not the same differential volume I am talking about.

I said that both pressure forces should act on the same differential fluid element and they clearly don't in this example since these fluid elements flow through DIFFERENT cross sections in period $dt$. We have two different fluid elements being subjected to different pressure forces.

 

[Dale]

force balance should be written on differential volume fluid which IS NOT a case in this derivation

No $A \ dx$ is a differential volume of fluid.

I said that both pressure forces should act on the same differential fluid element and they clearly don't in this example since these fluid elements flow through DIFFERENT cross sections in period dt. We have two different fluid elements being subjected to different pressure forces.

No, it is one fluid element. I am not sure why you think otherwise.

By "both pressure forces" you mean the pressure force on the "upstream" side and the "downstream" side, right? If so, then how can you think they are acting on different fluid elements.

 

[russ_watters]

Pressure forces on two cross sections act on system or volume element which doesn't have differential volume. What you mentioned about differential volume $Adx$ which flows through any cross section in time $dt$ is not the same differential volume I am talking about.

I think it is.

I said that both pressure forces should act on the same differential fluid element and they clearly don't in this example since these fluid elements flow through DIFFERENT cross sections in period dt.

Continuity demands that volumetric flow through a cross section must be the same for both locations and same dt. The cross section and velocity change by the same proportion.

 

[Dario56]

No $A \ dx$ is a differential volume of fluid.

That is true, but that is not the point. Point is these fluid elements aren't the same. It is like trying to sum forces acting on two DIFFERENT bodies and applying Newton's 2nd law.

 

[Dario56]

I think it is.

Continuity demands that volumetric flow through a cross section must be the same for both locations and same dt. The cross section and velocity change by the same proportion.

Yes, these volumes will certainly have same value assuming incompressible flow. However, they aren't the same body of fluid. It is like trying to sum forces acting on two different bodies.

 

[Dale]

Point is these fluid elements aren't the same. It is like trying to sum forces acting on two DIFFERENT bodies and applying Newton's 2nd law.

By "these fluid elements" I assume you refer to the drawing where they show one parcel in one section of tube and another parcel in a different section of tube with a different diameter and height. If so, then where do they sum forces on those two different bodies? I don't see anywhere that is done.

 

[Dario56]

No $A \ dx$ is a differential volume of fluid.

That is true, but that is not the point.

No $A \ dx$ is a differential volume of fluid.

No, it is one fluid element. I am not sure why you think otherwise.

By "both pressure forces" you mean the pressure force on the "upstream" side and the "downstream" side, right? If so, then how can you think they are acting on different fluid elements.

Yes, I refer to these pressure forces. These two fluid elements aren't the same body of fluid, they are like two different bodies. Like weight 1 and weight 2 in physics problems. Their value of volume is the same because of mass conservation and non - compresibility (just like masses of weight 1 and weight 2 may the same), but they are distinct fluid elements flowing through different cross sections in the same time. Also, as they flow, they are subjected to different forces acting on them.

 

[Dario56]

By "these fluid elements" I assume you refer to the drawing where they show one parcel in one section of tube and another parcel in a different section of tube with a different diameter and height. If so, then where do they sum forces on those two different bodies? I don't see anywhere that is done.

It is true that forces aren't summed in these derivations. However, to apply work - energy principle, we want to find work of resultant force or sum of works of all forces acting on some body - other one is applied in this derivation. What I don't get, what does exactly constitute our body or system in this derivation since to be able to apply work - energy theorem is to firstly define our body or system, write force balance on it and than calculate net work done. If that system is volume of fluid between two cross sections, this has no sense because in that way we can only track how center of mass of that system moves in time and space, not to explain how fluid accelerates between two cross sections. Because net force according to Newton's 2nd law causes acceleration which value is actually acceleration of system's CENTER OF MASS and when fluid accelerates between two cross sections, this isn't tracking of COM.

 

[Arjan82]

You are actually right. If you do derive Bernoulli using only differential equations and thus fluid parcels (this is indeed possible) you need at some point need to assume that the two parcels you analyse are on the same streamline. This is a necessary assumption for the derivation of the Bernoulli equation from the differential form.

But often it is the case that all streamlines start from the same volume of fluid at the same pressure and velocity (and density and temperature, height, etc. whatever you take into account in your analysis) and therefore all start with the same Bernoulli constant. This constant then doesn't change in the entire body of fluid (for which Bernoulli is valid of course). This is often why the analysis for differential volumes like Adx is still valid.

 

[russ_watters]

Yes, these volumes will certainly have same value assuming incompressible flow. However, they aren't the same body of fluid. It is like trying to sum forces acting on two different bodies.

This is a distinction without a difference. The point here is that the fluid flow is steady and along a streamline so it actually doesn't matter if it is one element at two different times or two different elements at the same time.

You are trying to describe a logic problem but where is the practical problem? What inconvenience does this cause?

 

[Dario56]

You are actually right. If you do derive Bernoulli using only differential equations and thus fluid parcels (this is indeed possible) you need at some point need to assume that the two parcels you analyse are on the same streamline. This is a necessary assumption for the derivation of the Bernoulli equation from the differential form.

But often it is the case that all streamlines start from the same volume of fluid at the same pressure and velocity (and density and temperature, height, etc. whatever you take into account in your analysis) and therefore all start with the same Bernoulli constant. This constant then doesn't change in the entire body of fluid (for which Bernoulli is valid of course). This is often why the analysis for differential volumes like Adx is still valid.

Problem for me is as follows. Fluid has different velocity on two cross sections. This requires acceleration. Acceleration requires force. This force has something to do with pressure difference on two cross sections. I am sure we are on the same page here. Derivations of Bernoulli's equation/principle from work - energy principle start with what I said. Work done by net force on the body or system equals change in its kinetic energy. In our example, work of gravity is zero as pipe is horizontal. Problem in these derivations is that they define system as volume of fluid between two cross sections. This has no sense because net force acting on that volume of fluid should cause its center of mass (COM) to accelerate, but that doesn't happen in fluids, it happens in solid bodies. Acceleration happen in sense that fluid has different velocity on two cross sections, but that can't be explained by force acting on volume of fluid between two cross sections because of reasons I gave. So, in my opinion, this derivation is wrong. It can be explained by looking at differential volume of fluid and calculating line integral of pressure gradient along the streamline only.

 

[russ_watters]

These two fluid elements aren't the same body of fluid, they are like two different bodies. Like weight 1 and weight 2 in physics problems. Their value of volume is the same because of mass conservation and non - compresibility (just like masses of weight 1 and weight 2 may the same), but they are distinct fluid elements flowing through different cross sections in the same time. Also, as they flow, they are subjected to different forces acting on them.

Bernoulli noticed an equivalence between them.

 

[Dario56]

This is a distinction without a difference. The point here is that the fluid flow is steady and along a streamline so it actually doesn't matter if it is 1 element at two different times or two different elements at the same time.

You are trying to describe a logic problem but where is the practical problem? What inconvenience does this cause?

This isn't about logic really, it is about understanding and correctly applying scientific principles. Why is it important if fluid flow is steady? That doesn't change that these fluid elements aren't the same. What principle in physics can back this claim?

 

[Dario56]

Bernoulli noticed an equivalence between them.

How? What principle in physics backs that these two elements are in fact the same body?

 

[Arjan82]

Actually Newton's second law is not about acceleration but about momentum. The 'real' 2nd law of Newton states that the change in momentum is equal to a force.

Remember that change in momentum = d(mv)/dt = mdv/dt + vdm/dt = sum of all forces. But for solids usually dm/dt is zero and dv/dt is of course acceleration. This results in the famous F=ma. But for fluids the term dm/dt is not necessarily zero.

So, in a case of a fluid you take a control volume stationary in space (this is actually not necessary, but makes integration a lot easier) then you apply Newton's second law by stating that the momentum flow into the volume (over it's boundaries) is equal to the momentum out of that volume plus the force applied on that volume (for example if one of the boundaries of that volume is a solid wall, but note that the pressure integrated over a boundary over which fluid flows is also a force which needs to be taken into account). If you apply this correctly than you end up with the Navier-Stokes equations.

 

[Arjan82]

This isn't about logic really, it is about understanding and correctly applying scientific principles. Why is it important if fluid flow is steady? That doesn't change that these fluid elements aren't the same. What principle in physics can back this claim?

Actually there is also a form of the Bernoulli equation which includes times derivatives.

 

[russ_watters]

Problem for me is as follows. Fluid has different velocity on two cross sections. This requires acceleration. Acceleration requires force. This force has something to do with pressure difference on two cross sections. I am sure we are on the same page here.

Yes.

...net force acting on that volume of fluid should cause its center of mass (COM) to accelerate, but that doesn't happen in fluids...

I don't know why you would think that's true. It's absolutely not. Fluids get forces applied and experience accelerations. Newton's laws requires it.

This isn't about logic really, it is about understanding and correctly applying scientific principles.

That's logic.

Why is it important if fluid flow is steady? That doesn't change that these fluid elements aren't the same. What principle in physics can back this claim?

Bernoulli's Principle.

Bernoulli found that given a certain set of starting assumptions, a certain mathematical constant remained constant at different times and locations in a fluid.

 

[Dario56]

Actually Newton's second law is not about acceleration but about momentum. The 'real' 2nd law of Newton states that the change in momentum is equal to a force.

Remember that change in momentum = d(mv)/dt = mdv/dt + vdm/dt = sum of all forces. But for solids usually dm/dt is zero and dv/dt is of course acceleration. This results in the famous F=ma. But for fluids the term dm/dt is not necessarily zero.

So, in a case of a fluid you take a control volume stationary in space (this is actually not necessary, but makes integration a lot easier) then you apply Newton's second law by stating that the momentum flow into the volume (over it's boundaries) is equal to the momentum out of that volume plus the force applied on that volume (for example if one of the boundaries of that volume is a solid wall, but note that the pressure integrated over a boundary over which fluid flows is also a force which needs to be taken into account). If you apply this correctly than you end up with the Navier-Stokes equations.

This is actually Cauchy equation. Navier - Stokes are than derived for isotropic and Newtonian fluids. This is all correct, but it doesn't answer my question if common derivation of Bernoulli's equation via work - energy principle is in fact wrong.

For stationary flow, dm/dt is zero. Mass of the fluid accumates nowhere.

 

[russ_watters]

This is all correct, but it doesn't answer my question if common derivation of Bernoulli's equation via work - energy principle is in fact wrong.

Not to be too pointed here, but you're claiming something is wrong with an established physics principle. Given a choice of where the problem might lie, I wouldn't pick Bernoulli or his principle. It's not a coincidence that the derivation produces Bernoulli's principle and that Bernoulli's principle works. It works because the equivalence he discovered is real.

 

[Arjan82]

This is actually Cauchy equation. Navier - Stokes are than derived for isotropic and Newtonian fluids. This is all correct, but it doesn't answer my question if common derivation of Bernoulli's equation via work - energy principle is in fact wrong.

For stationary flow, dm/dt is zero. Mass of the fluid accumates nowhere.

Are we getting picky here? But you are absolutely right, it's the Cauchy equation. And of course for stationary flow dm/dt is zero, all d/dt terms are zero, that's the definition of stationary flow...

Looking at accelerating centers of masses of a body of water is a bit of a crude way to look at a fluid flows. But I think it is still correct when you do not allow any fluid to cross the control volume (at least in an average sense, things get very messy very quickly when turbulence is involved, also, when the control volume deforms in such a way that it becomes self-intersecting or disjoint, things get very messy indeed...). Why would that view be wrong*? when there is no flow crossing the boundaries the COM is perfectly well defined at all instances and you can talk about its acceleration. You can also perfectly well talk about forces acting on your control volume. So I don't see why that view is wrong.

*)[edit] at least for engineering purposes, I mean, the analysis in the video posted earlier is really valid for plug flow, which doesn't really exist in reality. But then again, for Bernoulli it is necessary to assume inviscid flow, so you cannot have any boundary layers anyway.

 

[Dale]

It is true that forces aren't summed in these derivations.

Then that objection doesn’t apply.

However, to apply work - energy principle,

This derivation doesn’t apply the work - energy principle.

This is very frustrating. I asked you for an example of a derivation that you object to. Any derivation that exemplified the problems. You posted a link to the derivation in Wikipedia. But so far that derivation does not do anything that you are complaining about.

At this point this thread is useless. I am going to close it. You are free to post a new thread on this topic. When you do so, you need to link to a specific derivation. You should provide exact quotes from the derivation highlighting the problematic statements. That would be a solid basis for a productive thread.