Working out Plane Structure via Powder X-ray Diffraction Multiplicand

[PandaKitten]

Homework Statement

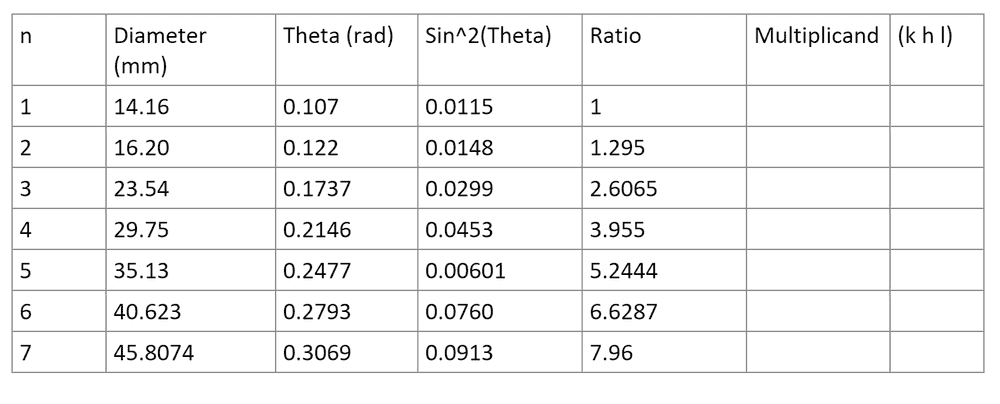
I need to work out the structure of NaCl using its Debye rings diameter and the equation below by working out its multiplicand and then assigning the appropriate plane structure to it.

Relevant Equations

(h^2+k^2+l^2)_min * (sin^2(theta_n))/(sin^2(theta_min)) = integer

Below is the measured values for the Debye rings I obtained. I have to multiply the ratio (which is (sin^2(theta_n))/(sin^2(theta_min))) by a multiplicand until I get an integer. However for the multiplicand and the values I measured I get 1, 3, 13, ??, 4, 8, ??. These should either correspond to a cubic structure (1,2,3,4,5...) a body centric structure (2,4,8,10..) or a face centric structure (3,4,8,11,12,16) but they don't correspond to any of them and also they should be in ascending size.

 

[etotheipi]

Do you know what the distance to the screen is, so we can check your calculations?

It's important to be careful to note that the radius of the Debye-Scherrer ring corresponds to an angle of $2\theta$ (and likewise the diameter of the Debye-Scherrer ring corresponds to an angle of $4 \theta$), if $\theta$ is the scattering angle. Did you take that into account?

Assuming you didn't make a mistake, the first four results at least are approximately in the ratio $3:4:8:11$ which is indeed what you'd expect from FCC, for the $(111)$, $(200)$, $(220)$ and $(311)$ planes respectively.

 

[PandaKitten]

Do you know what the distance to the screen is, so we can check your calculations?

It's important to be careful to note that the radius of the Debye-Scherrer ring corresponds to an angle of $2\theta$ (and likewise the diameter of the Debye-Scherrer ring corresponds to an angle of $4 \theta$), if $\theta$ is the scattering angle. Did you take that into account?

Assuming you didn't make a mistake, the first four results at least are approximately in the ratio $3:4:8:11$ which is indeed what you'd expect from FCC, for the $(111)$, $(200)$, $(220)$ and $(311)$ planes respectively.

32.5mm

 

[etotheipi]

Your work so far looks correct in that case. Here's what I think, denoting $N:= h^2 + k^2 + l^2$:

It's quite possible that the (311) & (222) peaks, and similarly the (311) & (420) peaks, were so close together that they just appear as a single ring each.

Nonetheless, your results can definitely be matched onto the FCC structure!

 

[PandaKitten]

Oh I see! I was given this equation that wasn't very well explained. So I assumed that the integer wasn't important and I should multiply them all by different multiplicands. But now I understand. Thank you so much.

 

[etotheipi]

Yeah, the key is that $\sin^2{(\theta)} / N$ is a constant, so the ratio of the $\sin^2{\theta}$'s of any two rows is the same as the ratio of the $N = h^2 + k^2 + l^2$'s of those two rows.

So in that sense, your table is a little misleading, because all the multiplicands are of course the same - in this case $3$ - and this multiplication only serves to display the ratios as nice whole numbers.