Working out the current and voltage in a circuit

[Bolter]

Homework Statement

Calculate the circuit's current and pd across a component

Relevant Equations

Ohm's law

Here are a few problems I have been trying which are shown below

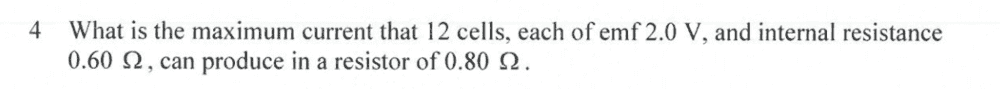
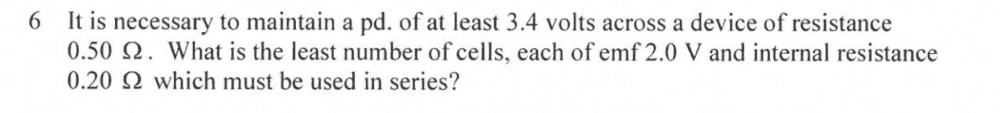
Here is what I have done

The correct answers for these Q's are:

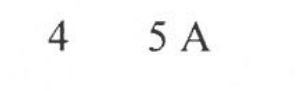
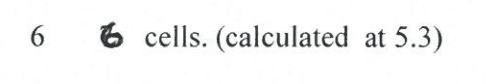
I'm not sure what I have done wrong for Q4, I assumed that all 12 cells were connected in series thus each individual emf sums up to 24V
Similarly the internal resistances must sum up to 7.2 ohms

Is there anything that I am missing for me to get a current value of 5 amps instead of 3 amps?

Any help would be really appreciated! Thanks

 

[haruspex]

I'm not sure what I have done wrong for Q4, I assumed that all 12 cells were connected in series

You just answered your own question.
Bear in mind that if the cells are in series then so are their internal resistances.

 

[DaveE]

Your calculation is correct, given the assumptions you made about the configuration of the circuit elements. Try some other arrangements to see if you've found the best one.

 

[Bolter]

Your calculation is correct, given the assumptions you made about the configuration of the circuit elements. Try some other arrangements to see if you've found the best one.

I believe that the maximum current can only be drawn out when all cells are attached in series, as this is the only way to produce the biggest EMF.
Arranging some or all cells in parallel would give a smaller EMF off

So biggest current has to be 3 amps then?

 

[BvU]

Similarly the internal resistances must sum up to 7.2 ohms

Hint: this also means that all current has to pass through all internal resistances -- not so favourable.

 

[BvU]

So biggest current has to be 3 amps then?

Nope

 

[Bolter]

Hint: this also means that all current has to pass through all internal resistances -- not so favourable.

Would this be a case of trial and error in figuring out what configuration the circuit elements must be to give a current of 5A?

So there has to be some parallel arrangement involved I suppose to decrease the total internal resistance since I=V/R, if R gets smaller then surely a bigger current is drawn. However that would also mean the emf, V gets smaller too?

 

[BvU]

as this is the only way to produce the biggest EMF.

biggest EMF at zero current - you found that 90% of that EMF is lost on internal resistances !

 

[BvU]

Would this be a case of trial and error in figuring out what configuration the circuit elements must be to give a current of 5A?

Basically: yes. I can't think of a 'golden rule'. In electronics there is somethinig called 'impedance matching', but for this exercise it doesn't work --- [edit] or does it ?

I, for example started with a try of all 12 parallel -- then the internal power loss is minimal, but the final EMF is too low. Fortunately there are only five sensible variations .

 

[Bolter]

Basically: yes. I can't think of a 'golden rule'. In electronics there is somethinig called 'impedance matching', but for this exercise it doesn't work --- [edit] or does it ?

I, for example started with a try of all 12 parallel -- then the internal power loss is minimal, but the final EMF is too low. Fortunately there are only five sensible variations .

I tried one other variation now where the cells are arranged in two parallel rows of 6, and this set up is then in series with the 0.8 ohm resistor

I get a new current of 4.62 A which is close to 5 A but not exactly 5 A

 

[BvU]

Keep going ...
You tried 12 x 1 with 24 V, 7.2 $\Omega$ internal resistance and 6 x 2 with 12 V, 1.8 $\Omega$ internal resistance.
I tried 1 x 12 with 2 V, 0.05 $\Omega$ internal resistance. Three down, two to go ...

 

[Bolter]

Keep going ...
You tried 12 x 1 with 24 V, 7.2 $\Omega$ internal resistance and 6 x 2 with 12 V, 1.8 $\Omega$ internal resistance.
I tried 1 x 12 with 2 V, 0.05 $\Omega$ internal resistance. Three down, two to go ...

Is this some sort of pattern that I'm not seeing?

I tried with 2 more possible set ups
Where one involved 4 parallel rows of 3 cells in series with fixed resistor
and another involved 3 parallel rows of 4 cells in series with fixed resistor

But the currents that I obtain from both are either 3.6 A or 3.75 A (not close to 5 A)

 

[hutchphd]

These are designated as 2V cells. (!)

 

[BvU]

get some rest !

 

[haruspex]

Would this be a case of trial and error

Not entirely.
In posts #10 and #12 you tried rectangular arrangements. You can generalise this to m by n, where mxn=12. It is not hard to figure out the current as a function of m.

 

[Bolter]

View attachment 256008

get some rest !

Oh shoot yes you're right!
My brain hasn't been processing properly which is why I mistook the value, actually was feeling tired

I tried with the emf of cell being 2.0 V now and get current to be 4.8 A for the circuit with 4 parallel rows of 3 cells
and 5 A with 3 parallel rows of 4 cells.

So the last configuration must be the one I am looking for to use, to generate a circuit current of 5 A

 

[Bolter]

Not entirely.
In posts #10 and #12 you tried rectangular arrangements. You can generalise this to m by n, where mxn=12. It is not hard to figure out the current as a function of m.

Right I now see, so all possible combinations I could have used are:

12 cells all in series
2 parallel rows of 6 cells
4 parallel rows of 3 cells
3 parallel rows of 4 cells
6 parallel rows of 2 cells

And then finally all 12 cells in parallel with each other so we have 12 rows then

so for mxn=12

I know m denotes the number of branches
and n denotes the number of cells in that branch

What do you mean when you say current can written as a function of m

I know that in parallel arrangements, current is known to split when it comes to an entry junction however same amount of current must leave at exit junction too. This is just Kirchhoff's 1st law that I am stating.

Looking at my case, I believe I will have equal amount of current flowing through all branches. This is since I'm dealing with identical cells all which has same number of cells on each branch. Current has to shared proportionately from resistance available in each row, right?

Is this the sort of information I have to use to formulate a function of m to give current?

 

[BvU]

And it so happens that in the 4 x 3 case the internal impedance is 0.8 $\Omega$ ...
Must be more than just a coincidence ...

 

[Bolter]

And it so happens that in the 4 x 3 case the internal impedance is 0.8 $\Omega$ ...
Must be more than just a coincidence ...

Yep, should really look into this. Would come into be nifty at times

 

[haruspex]

What do you mean when you say current can written as a function of m

Let the current in each branch be I and end to end voltage be V.
If the external resistance is R, what equation relates V, I, m and R?
If the internal resistance is r and the internal voltage is v, what equation relates V, v, n, I and r?

 

[Bolter]

Let the current in each branch be I and end to end voltage be V.
If the external resistance is R, what equation relates V, I, m and R?
If the internal resistance is r and the internal voltage is v, what equation relates V, v, n, I and r?

Looking at the whole circuit, isn't external resistance R just R = V/I. I can't see how m gets related

And focusing on one single branch, where let's say there are 'n' number of cells in that branch

v = nIr
so V + v = IR + nIr = I (R + nr)

Edit: Is V = mIR?

As a same current I, is flowing through 'm' number of branches, all these currents then get combined at the the end of a node to produce a current of mI. Thus R = V/mI

 

[haruspex]

v = nIr

No. In each cell in the line you have an emf of v partly used up by the emf needed to push a current I through internal resistance r.
But it isn't all used up or V would be 0.

Is V = mIR?

Yes.

 

[Bolter]

No. In each cell in the line you have an emf of v partly used up by the emf needed to push a current I through internal resistance r.
But it isn't all used up or V would be 0.

Yes.

Hmm ok so terminal voltage (V) + lost volts (v) = emf

Then v = emf – V

v = emf – mIR

I would express emf as 2n, where 2 is the emf of a single cell and 'n' is the number of cells in that line

Therefore v = 2n – mIR?

 

[haruspex]

Hmm ok so terminal voltage (V) + lost volts (v) = emf

Then v = emf – V

v = emf – mIR

I would express emf as 2n, where 2 is the emf of a single cell and 'n' is the number of cells in that line

Therefore v = 2n – mIR?

No, I defined v as the nominal voltage (2 Volts) of each cell. Of that, Ir is lost in each cell leaving ...? Adding that up for the line of n cells gives ...? Which is equal to what other variable?

 

[Bolter]

No, I defined v as the nominal voltage (2 Volts) of each cell. Of that, Ir is lost in each cell leaving ...? Adding that up for the line of n cells gives ...? Which is equal to what other variable?

So it should be nv – nIr = V

factoring out n gives n(v – Ir) = V

 

[haruspex]

So it should be nv – nIr = V

factoring out n gives n(v – Ir) = V

Right.
Combine that with your other equation for V to get mI (the total current) in terms of n, m, v, r and R.

 

[Bolter]

Right.
Combine that with your other equation for V to get mI (the total current) in terms of n, m, v, r and R.

Combining it, I get this,
where I do get 5A once I let m = 3 and n = 4

 

[haruspex]

Combining it, I get this,
where I do get 5A once I let m = 3 and n = 4

View attachment 256077

Yes, but better still you can avoid having to guess. How do you find the maximum of a function?

 

[Bolter]

Yes, but better still you can avoid having to guess. How do you find the maximum of a function?

Work out the first order derivative of that function and equate it to zero. Though don't we have 2 unknowns in the function which are m and n? so you couldn't find either?

 

[haruspex]

Work out the first order derivative of that function and equate it to zero. Though don't we have 2 unknowns in the function which are m and n? so you couldn't find either?

The product mn is fixed, so there is only one independent variable.