Worst-case power consumed by a circuit with MOSFETs

[zenterix]

Homework Statement

Consider the circuit depicted below. Use the Switch-Resistor model for the MOSFETs.

Assume $R_6=R_7=10\mathrm{k\Omega}$, the threshold voltage for the MOSFETs is $\mathrm{2V}$, and the resistance of the MOSFET in its ON state is $\mathrm{1k\Omega}$.

Compute the worst-case power consumed by this circuit.

Relevant Equations

$P=iV$

Here is the circuit.

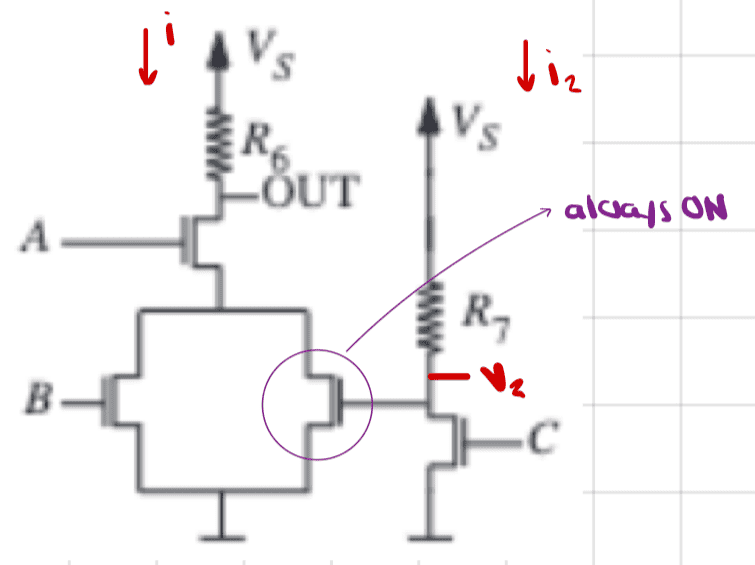
Note that no current flows between the left and right sides of the circuit: their only relationship happens through the MOSFET that is parallel to B.

There are eight cases to consider: all the combinations of ON/OFF for the three MOSFETs.

Here is a summary of the eight cases according to my calculations

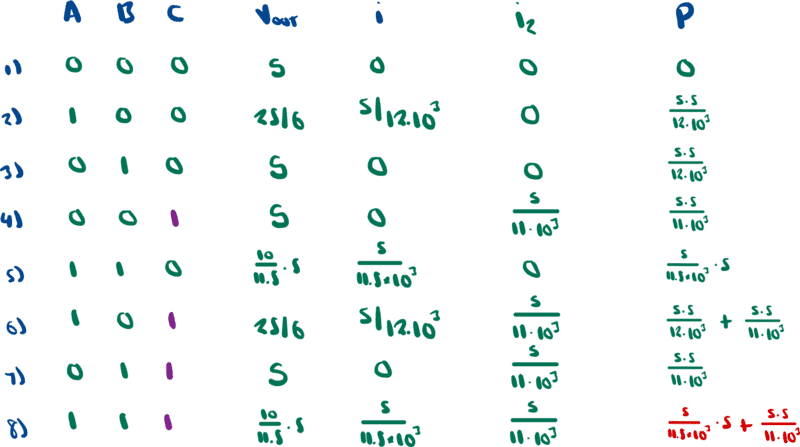
It seems that the highest power consumption occurs when all MOSFETs are on.

Here is more in depth explanation of how the table above was created.

It seems that whether MOSFET C is on or off, the voltage at the node right above it (beneath resistor R7) is higher than $V_T=\mathrm{2V}$.

Thus, the MOSFET in parallel with B is always on.

Let's consider just the left side of the circuit for now.

If $A$ is off, then no current flows so $i=0$.

Suppose A is on.

Then we have two cases: B on, B off.

If B is on, then the left side of the circuit becomes

$i=\frac{5}{11.5\cdot 10^3}\text{A}$ and $v_{OUT}=\frac{10}{11.5}\cdot 5\text{V}$.

Power consumed by this subcircuit is $i\cdot V_S=5\cdot\frac{5}{11.5\cdot 10^3}\mathrm{\frac{J}{S}}$.

If, on the other hand, B is off then the only difference is that the resistance that is $1/2\mathrm{k\Omega}$ above becomes $1\mathrm{k\Omega}$.

Thus, $i=\frac{5}{12\cdot 10^3}\mathrm{A}$ and $v_{OUT}=\frac{10}{12}\cdot 5=\frac{25}{6}\text{V}$.

Now consider the right side of the circuit.

Suppose $C$ is on. Then the current on the right side (call it $i_2$) will be $i_2=\frac{5\text{V}}{11\cdot 10^3}\text{A}$.

If $C$ is off, then no current flows on the right side.

Finally, to obtain power consumption I simply computed $P=i\cdot V_S+i_2\cdot V_S$ for all eight cases.

Is this the correct calculation?

 

[hutchphd]

The ON resistance of the MOSFET is kilo-ohms??? Seems odd.

 

[zenterix]

Here is the problem statement in full. From this problem set of MIT OCW's 6.002

The cited exercise from Agarwal's books is

and here is Figure 6.59(c)

Thus, the ON resistance is indeed 1 kilo-ohm.