- #1
jonny_d
- 3
- 2
Greetings everybody. This is my first post and I am looking for help with a little math/geometry/engineering problem. This has been a real brain buster for my colleague and I the past couple days so I am hoping somebody can help. I am not sure if this is the best section for it, but it applies to an engineering design I am working on so I will put it here...I need to come up with a math model for the following problem:
A ribbon is wrapped around a cone. The cone rotates around it's axis as a machine traverses down the length of the cone (parallel to the cone axis) while applying even tension through the cross section of the ribbon. The ribbon material is of high modulus and it can be assumed to have no compliance except in the direction that it bends on to the surface of the cone. Also the ribbon must lay flat on the surface of the cone with no wrinkling or buckling of the material.
Here is a quick sketch of the problem:
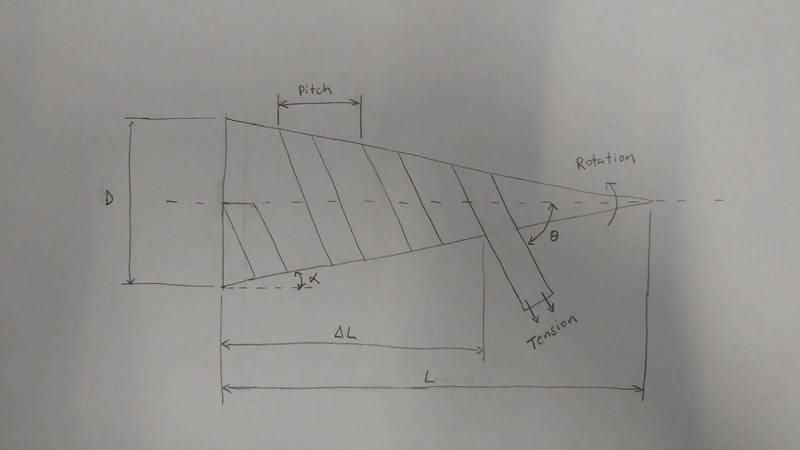
Through experimentation and intuition I have determined that the wrap angle (theta) and the pitch will change as the wrap progresses. Specifically, the wrap angle will increase and the pitch will decrease as shown in the image. So for the machine to work, it will need to change the angle that it grips the material and compensate for the changing pitch as it translates along the length of the cone.
For a math model to represent the system I am thinking that it will need the following as I/O:
Inputs: cone taper angle (alpha), cone base diameter (D), initial wrap angle (theta), delta L
Outputs: pitch and wrap angle at the given delta L
I would also be interested in any advice on how to accurately model this in CAD in such a way that the ribbon is not deformed. I have access to SolidWorks and Catia.
Final note: the cone angle in my sketch is greatly exaggerated, and in actuality it will be a tapered cylinder, but I am considering it a cone here for simplicity. The actual taper is less than a degree over a length of 40 feet. This may sound insignificant but experimentation has shown that it truly matters for the application.
So does anyone want to take a crack at this? Thanks in advance!
A ribbon is wrapped around a cone. The cone rotates around it's axis as a machine traverses down the length of the cone (parallel to the cone axis) while applying even tension through the cross section of the ribbon. The ribbon material is of high modulus and it can be assumed to have no compliance except in the direction that it bends on to the surface of the cone. Also the ribbon must lay flat on the surface of the cone with no wrinkling or buckling of the material.
Here is a quick sketch of the problem:
Through experimentation and intuition I have determined that the wrap angle (theta) and the pitch will change as the wrap progresses. Specifically, the wrap angle will increase and the pitch will decrease as shown in the image. So for the machine to work, it will need to change the angle that it grips the material and compensate for the changing pitch as it translates along the length of the cone.
For a math model to represent the system I am thinking that it will need the following as I/O:
Inputs: cone taper angle (alpha), cone base diameter (D), initial wrap angle (theta), delta L
Outputs: pitch and wrap angle at the given delta L
I would also be interested in any advice on how to accurately model this in CAD in such a way that the ribbon is not deformed. I have access to SolidWorks and Catia.
Final note: the cone angle in my sketch is greatly exaggerated, and in actuality it will be a tapered cylinder, but I am considering it a cone here for simplicity. The actual taper is less than a degree over a length of 40 feet. This may sound insignificant but experimentation has shown that it truly matters for the application.
So does anyone want to take a crack at this? Thanks in advance!















