- #36
I like Serena
Homework Helper
MHB
- 16,336
- 258
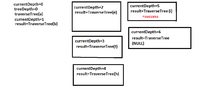
evinda said:Do we have to use a new variable $k$ or could we also do it in an other way? (Thinking)
What do you want to use [m]k[/m] for? (Wondering)
Its name doesn't say anything about its purpose, and as it is currently used, it doesn't seem to do anything useful.