Writing the charge density in the form of the Dirac delta function

[approx12]

Homework Statement

Given a square with side length $a$ and a surface charge of $\sigma$ for $y>0$ and $\epsilon \sigma$ for $y<0$, write down the charge density $\rho(\vec{x})$ in terms of the dirac delta function.

Relevant Equations

$\rho(\vec{x})=\sigma \cdot...$

Hey guys! Sorry if this is a stupid question but I'm having some trouble to express this charge distribution as dirac delta functions.

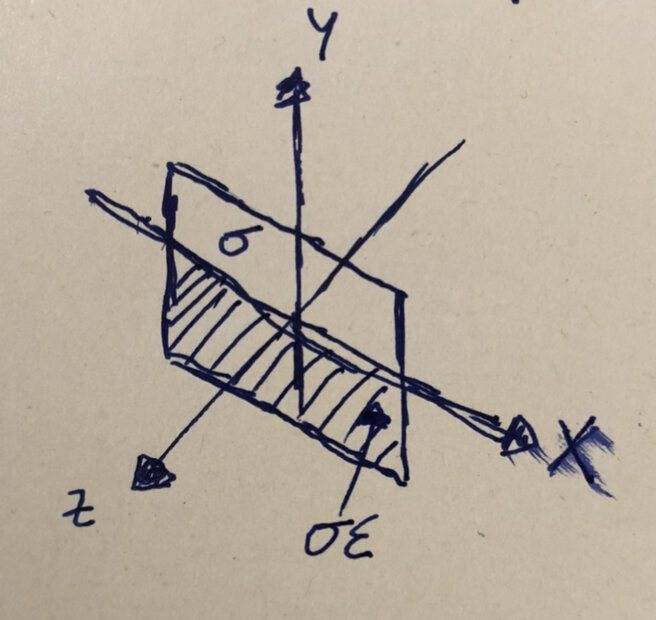
I know that the charge distribution of a circular disc in the $x-y$-plane with radius $a$ and charge $q$ is given by $$\rho(r,\theta)=qC_a \delta(\theta-\pi/2)\delta(r-a)$$ (with $C_a$ being a fitting constant). Based on this I've tried to write down the charge distribution of the rectangle as follows: $$\rho(\vec{x})=C\sigma(\delta(x-a/2)+\delta(y-a/2)+\epsilon \delta(x-a/2)+\epsilon \delta(y+a/2))$$ (With $C$ and $C_{\epsilon}$ being fitting constants)

I do not know though if this is a correct way to write it down or if I have to approach it in some other way. It would be awesome if anyone could give me some strategy on how to think about problems like this. Thank you!

 

[vanhees71]

First write down the definition of your $xy$-plane in the form $\Phi(\vec{x})=0$. Then think again about how the generalized charge density must look!

 

[approx12]

First write down the definition of your $xy$-plane in the form $\Phi(\vec{x})=0$. Then think again about how the generalized charge density must look!

Hi, thanks for taking the time to reply! I think I'm not quite sure what you mean with $\Phi(\vec{x})=0$, do you mean the electric potential or some plane equation (that would be $z=0$ for the $xy$-plane I guess). I also thought about writing the charge density in combination with the heaviside function. For example: $$\rho=C\sigma\delta(z)\theta(a/2-|x|)\theta(a/2-y)+...$$ Would a approach like this make sense in this problem?

 

[vanhees71]

I had the general formula
$$\rho(\vec{x})=\sigma(\vec{x}) |\vec{\nabla} \Phi(\vec{x})| \delta[\Phi(\vec{x})]$$
in mind. In your case $\Phi(\vec{x})=z$, $|\vec{\nabla} \Phi|=|\vec{e}_z|=1$.

 

[approx12]

I had the general formula
$$\rho(\vec{x})=\sigma(\vec{x}) |\vec{\nabla} \Phi(\vec{x})| \delta[\Phi(\vec{x})]$$
in mind. In your case $\Phi(\vec{x})=z$, $|\vec{\nabla} \Phi|=|\vec{e}_z|=1$.

Oh, thank you, I was not familiar with this general formula. Are there maybe any references to it in some books or online so I can look it up?

But to the problem: So, it looks like the charge density reduces in my case to: $$\rho=\sigma\delta(z)$$ Which, I think, refers to a surface charge placed in the $xy$ plane. So does the confinement of the surface charge to the rectangle only happen by constraining $-a/2<x<a/2$ and $-a/2<y<a/2$? Thanks again for your patience!

 

[vanhees71]

I don't know, from where I got this formula, but it's not too difficult to prove. Given is the scalar field $\Phi(\vec{x})$, defined in a neighborhood of the surface, which is defined implicitly by $\Phi(\vec{x})=0$. Now we define iso-$\Phi$ surfaces by parameters $(q_1,q_2,q_3)$ in such a way that $\Phi[\vec{x}(q_1,q_2,q_3)]=q_3$. Thus these surfaces are parametrized by $q_1$ and $q_2$ and the surface is determined by the value of $q_3$ (in an intervall containing $q_3=0$).

Now it's clear that $\partial_{q_1} \vec{x}$ and $\partial_{q_2} \vec{x}$ span the tangent surfaces on the $\Phi=\text{const}$ surfaces and $\vec{\nabla} \Phi$ is always perpendicular to these tangent surfaces and $\partial_{q_3} \vec{x} \cdot \vec{\nabla} \Phi=1$. Let $\vec{n}$ denote the unit normal vectors at the surface such that $\vec{n} \cdot \vec{\nabla} \Phi=|\vec{\nabla} \Phi|$.

Now we calculate the charge within some volume element containing part of the surface $\Phi=q_3=0$ in its interior using $\rho(\vec{x})=\sigma|\vec{\nabla} \Phi| \delta(\Phi)$ as charge density, defined by the parameters $(q_1,q_2,q_3) \in D \subseteq \mathbb{R}^3$:
$$Q_V = \int_D \mathrm{d}^3 q (\partial_{q_3} \vec{x}) \cdot (\partial_{q_1} \vec{x} \times \partial_{q_2} \vec{x}) |\vec{\nabla} \Phi| \delta(q_3) \sigma$$
$$= \int_D \mathrm{d}^3 q |\partial_{q_1} \vec{x} \times \partial_{q_2} \vec{x}| (\partial_{q_3} \vec{x}) \cdot \vec{n} |\vec{\nabla} \Phi| \delta(q_3) \sigma$$
$$= \int_D \mathrm{d}^3 q |\partial_{q_1} \vec{x} \times \partial_{q_2} \vec{x}| (\partial_{q_3} \vec{x}) \cdot \vec{\nabla} \Phi \delta(q_3) \sigma $$
$$= \int_D \mathrm{d} q_3 \mathrm{d}^2 f \sigma \delta(q_3)=\int_F \mathrm{d}^2 f \sigma,$$
where $F$ is the surface defined by $q_3=\Phi(\vec{x})=0$. This shows that the above defined $\rho$ is equivalent to a surface-charge density $\sigma$.

Obviously the surface density $\sigma(\vec{x})$ needs only be defined along the surface and is given by your problem in #1.