Solving the Heart Curve Equation: 'y =

[pairofstrings]

TL;DR Summary

I found the following heart curve on web:
x[SUP]6[/SUP] + 3x[SUP]4[/SUP]y[SUP]2[/SUP] - 3x[SUP]4[/SUP] + 3x[SUP]2[/SUP]y[SUP]4[/SUP] - x[SUP]2[/SUP]y[SUP]3[/SUP] - 6x[SUP]2[/SUP]y[SUP]2[/SUP] + 3x[SUP]2[/SUP] + y[SUP]6[/SUP] - 3y[SUP]4[/SUP] + 3y[SUP]2[/SUP] = 1

Hello.

I am trying to write the equation of this heart curve as 'y = '.
So the following is my attempt to form that equation: 1 = 1/y (x⁶y + 3x⁴y³ - 3x⁴y + 3x²y⁵ - x²y⁴ - 6x²y³ + 3x²y + y⁷ - 3y⁵ + 3y³)

Here, the graph of the above equation looks like this:

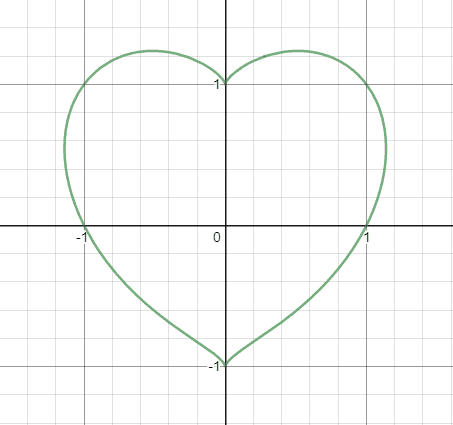
Now, next I should write it as 'y = ' but the problem is as I rewrite the above equation as y = x⁶y + 3x⁴y³ - 3x⁴y + 3x²y⁵ - x²y⁴ - 6x²y³ + 3x²y + y⁷ - 3y⁵ + 3y³

I get the curve correctly but there is a line going across the curve horizontally like this:

Question: How do I get rid of the line (green) from the above heart curve?

Thank you!

 

[Office_Shredder]

Why do you want it as y= something? The other side includes y as well so you haven't actually made your life easier.

 

[DrClaude]

There is no a single value of y for any given x, hence in is not a function of x, $y \neq f(x)$. It is a parametric equation, same as $x^2 + y^2 = 1$ to describe a circle.

 

[pairofstrings]

There is no a single value of y for any given x, hence in is not a function of x, y≠f(x). It is a parametric equation, same as x2+y2=1 to describe a circle.

I am not able to understand "There is no single value of 'y' for any given 'x'".

I see that you've said that it is a parametric equation.
I searched web to find different types of equations.
I found:

Different Types of Equations

• Quadratic Equation.
• Linear Equation.
• Radical Equation.
• Exponential Equation.
• Rational Equation.

In the list above there is no mention that there is a parametric equation as one of the types of equation.

Can you please list different types of equation?

Thanks!

 

[Office_Shredder]

You can't write this as y=f(x) because given an x value, there are multiple y values (pick an x value, draw a vertical line z observe you often hit the curve twice).

You wrote something that is of the form y=f(x,y). When you did so you introduced an extra factor of y which is why you got that line. It might be fixable, but first, why do you even care about writing it in this form?

To simplify the example, suppose you have the vertical line x=1. You can multiply both sides by y and get y=xy. This has the vertical line as a solution, but also y=0 is a solution for any x so you will add a horizontal line to the graph. It also doesn't give y as a function of x (no such function exists!) So it's not clear why you would want to do this anyway.

 

[Mark44]

n the list above there is no mention that there is a parametric equation as one of the types of equation.

You must not have searched very hard. Here's a wiki page on parametric equations: Parametric equation - Wikipedia

 

[mfb]

Different Types of Equations

• Quadratic Equation.
• Linear Equation.
• Radical Equation.
• Exponential Equation.
• Rational Equation.

In the list above there is no mention that there is a parametric equation as one of the types of equation.

Can you please list different types of equation?

That's a different "type of type".
As an analogy, you can group cars into red cars, blue cars, white cars, ... and you'll never find a Mazda in that list, because grouping cars by manufacturer is a different list.

The types you found are all descriptions how e.g. y can depend on x - if every value of x leads to a unique value of y.
In a parametric equation (or set of equations) you add a new variable - a parameter - and then have x and y both depend on that parameter. In that case a single value of x can have two or more corresponding values of y.

I searched web to find different types of equations.

Just clicking the link you quoted would have been sufficient.

@DrClaude: It is not a parametric equation. Where is the parameter? It is locally an implicit function, however.

 

[pairofstrings]

The last one is Parametric Form.
(x-m)² + (y-n)² = r² is standard form of an equation of circle.
What is Input form?
a x² + b xy + c y² + d x + e y = f is general form of equation of circle.
What happens if there is no 'b xy' in general form of equation of circle?
What is 'b xy'?

 

[pairofstrings]

In the equation below (heart curve):

In the heart curve, I see that there is term like 'b xy' occurring too often.
To understand what 'b xy' is, let's look into the equation: 1 = x + y + xy.

1 = x + y + xy; it means x = 1, y = 1, and xy = 1
The graph looks like this for the equation that has no 'xy' in the equation 1 = x + y.

To plot x = 1 I can move 1 unit to right and to plot y = 1 I can move 1 unit up.
Hence, the following curve.

Now, how to move with 'xy' in 1 = x + y + xy the way I moved with x = 1 and y = 1 in 1 = x + y (I moved 1 unit to right and 1 unit up here, how will I move with xy here) to get the following curve? Why the impact of 'xy' in the equation 1 = x + y + xy is the way it is in the following graph? How is 'xy' in the equation 1 = x + y + xy affecting the graph 1 = x + y? How do I move with 'xy' (in equation 1 = x + y, I moved 1 unit right and 1 unit up, therefore it's 1 = x + y)? How do I move with 'xy' in 1 = x + y + xy?

Thanks.

 

[Mark44]

What is Input form?

No idea. I don't know what program you are using. I suggest that you read the documentation for this program

a x² + b xy + c y² + d x + e y = f is general form of equation of circle.

No, it is not. This is the general form of what's called a conic section. Depending on the values of the coefficients a, b, c, d, e, and f, the equation could be that of a circle, ellipse, parabola, or hyperbola or even a straight line. Some calculus textbooks include a section on analytic geometry, which would discuss these kinds of figures.

What happens if there is no 'b xy' in general form of equation of circle?
What is 'b xy'?

The b coefficient determines whether and how much a basic conic section has been rotated. If b = 0, there has been no rotation.

 

[Mark44]

In the heart curve, I see that there is term like 'b xy' occurring too often.
To understand what 'b xy' is, let's look into the equation: 1 = x + y + xy.

1 = x + y + xy; it means x = 1, y = 1, and xy = 1

Clearly this is not true.
If x = 1, y = 1, then xy = 1, so you have 1 = 1 + 1 + 1, which is not true.

To plot x = 1 I can move 1 unit to right and to plot y = 1 I can move 1 unit up.
Hence, the following curve.

Well, the graph is correct, but your analysis of how to get it is incorrect. If you aren't able to figure out how to graph the simple equation x + y = 1 without using computer software, you are completely wasting your time trying to figure our what the graph of x + xy + y = 1 looks like.

 

[Vanadium 50]

the equation could be that of a circle, ellipse, parabola, or hyperbola or even a straight line.

Or two straight lines!

 

[Mark44]

Or two straight lines!

I thought of that situation, but didn't include it, given the level of knowledge of the OP. That case would technically be a degenerate hyperbola, which in the simplest form (i.e., unrotated) would be $x^2 - y^2 = 0$. This equation is equivalent to $y^2 - x^2 = 0$

 

[pairofstrings]

Are we using PEDMAS or BODMAS in the following equation to get the heart curve graph?
Are we practicing PEDMAS or BODMAS in the following equation to obtain the heart curve graph?
Are we adhering to PODMAS or BODMAS in the following equation to obtain the heart curve graph?

Equation:
x⁶ + 3x⁴y² - 3x⁴ + 3x²y⁴ - x²y³ - 6x²y² + 3x² + y⁶ - 3y⁴ + 3y² = 1

 

[Office_Shredder]

I've never heard of bodmas before but Google says it's the same as pemdas. So I guess the answer is... Yes.

 

[pairofstrings]

You wrote something that is of the form y=f(x,y). When you did so you introduced an extra factor of y which is why you got that line. It might be fixable, but first, why do you even care about writing it in this form?

The graph of the equation 1 = x + y is easy to draw. It says 'x' is 1 and 'y' is 1.
Therefore, I can plot the point at x = 1 and y = 1.

For the graph of the equation 1 = x y is there any short method to plot it?

 

[Office_Shredder]

(1,1) is not a point on the curve 1=x+y so I'm not sure what you mean there.

 

[Mark44]

The graph of the equation 1 = x + y is easy to draw. It says 'x' is 1 and 'y' is 1.
Therefore, I can plot the point at x = 1 and y = 1.

NO!
You've already said this, and I answered it a month ago, in post 11.

For the graph of the equation 1 = x y is there any short method to plot it?

wolframalpha...
But I would recommend you get a precalculus textbook, one that discusses how to graph simple functions and geometric curves.

If you don't know how to sketch a graph of x + y = 1, you have absolutely no hope of being able to graph something way more complicated like the one you started this thread with.

 

[Mark44]

I think we're done here, so am closing this thread. It's pointless to discuss the graph of a fairly high-degree polynomial when the OP doesn't understand how to graph a straight line.

@pairofstrings, after you have studied or reviewed how to graph simple curves, please start a new thread.