- #1
Slereah
- 7
- 0
I am currently trying to demonstrate by hand the various Clebsch-Gordan coefficients for the product of particles of various spins, using (mostly) the formalism of Young tableaux. For simple cases, so far, it has worked okay (that is, ½x½) , but trying for bigger ones (1x½, 3/2x½ and 1x1, for instance), I run into problems.
For instance, for ½x½, the Young tableaux are just the symmetrisation of the two spinors and the antisymmetrisation, so the decomposition is just
[itex]\psi_a \xi_b = \left( \!\!\begin{array}{cc}
\psi_+ \chi_+&\frac{1}{2}(\psi_+ \chi_- + \psi_- \chi_+)\\
\frac{1}{2}(\psi_+ \chi_- + \psi_- \chi_+)&\psi_- \chi_-
\end{array}\! \right) + \frac{1}{2}\left( \!\!\begin{array}{cc}
0&1\\
-1&0
\end{array}\! \right)(\psi_+ \chi_- - \psi_- \chi_+)[/itex]
Which, once normalized, gives the correct CG coefficients, and their sum gives back indeed the original product. Problems appear with higher spins, though, and I think they stem from the different ways you can have the various mixed symmetry terms.
For 1x½, for instance, the tableaux are just :
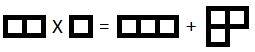
The first one is full symmetrisation on all three indices, the second is a mix of symmetrisation and antisymmetrisation. As the full symmetrisation is completely symmetric, there is only one of them, and so have no problems with such terms, and all the CG coefficients are good, but mixed terms pose a bigger problem. I tried doing the most obvious thing for the second term, and just have the two upper cells represent the two first indices and the second row the third, or the first cell the spinor and the other two the vector, different combinations of the various mixed terms possible, but none of it seems to work, as it does not give the correct CG coefficients and/or the terms do not add up to the original product.
Of course, what I can do is just 1x½ and substract the fully symmetric term. Which is :
[itex]A_{ab} \psi_c - A_{(ab} \psi_{c)} = A_{ab} \psi_c - \frac{1}{3}(A_{ab} \psi_c+A_{ac} \psi_b + A_{cb} \psi_a) = \frac{1}{3}(2 A_{ab} \psi_c-A_{ac} \psi_b - A_{cb} \psi_a) [/itex]
Which gives the correct CG coefficients and all, but this method only works here (and for 3/2x½), since above that, there are multiple mixed symmetry terms.
The fact that it contains a 1/3 factor bothers me, since I always find 1/4 with the tableaux, since they are symmetrisation and antisymmetrisation of two terms.
So what is the correct way of transforming a Young tableau into the equivalent tensors?
For instance, for ½x½, the Young tableaux are just the symmetrisation of the two spinors and the antisymmetrisation, so the decomposition is just
[itex]\psi_a \xi_b = \left( \!\!\begin{array}{cc}
\psi_+ \chi_+&\frac{1}{2}(\psi_+ \chi_- + \psi_- \chi_+)\\
\frac{1}{2}(\psi_+ \chi_- + \psi_- \chi_+)&\psi_- \chi_-
\end{array}\! \right) + \frac{1}{2}\left( \!\!\begin{array}{cc}
0&1\\
-1&0
\end{array}\! \right)(\psi_+ \chi_- - \psi_- \chi_+)[/itex]
Which, once normalized, gives the correct CG coefficients, and their sum gives back indeed the original product. Problems appear with higher spins, though, and I think they stem from the different ways you can have the various mixed symmetry terms.
For 1x½, for instance, the tableaux are just :
The first one is full symmetrisation on all three indices, the second is a mix of symmetrisation and antisymmetrisation. As the full symmetrisation is completely symmetric, there is only one of them, and so have no problems with such terms, and all the CG coefficients are good, but mixed terms pose a bigger problem. I tried doing the most obvious thing for the second term, and just have the two upper cells represent the two first indices and the second row the third, or the first cell the spinor and the other two the vector, different combinations of the various mixed terms possible, but none of it seems to work, as it does not give the correct CG coefficients and/or the terms do not add up to the original product.
Of course, what I can do is just 1x½ and substract the fully symmetric term. Which is :
[itex]A_{ab} \psi_c - A_{(ab} \psi_{c)} = A_{ab} \psi_c - \frac{1}{3}(A_{ab} \psi_c+A_{ac} \psi_b + A_{cb} \psi_a) = \frac{1}{3}(2 A_{ab} \psi_c-A_{ac} \psi_b - A_{cb} \psi_a) [/itex]
Which gives the correct CG coefficients and all, but this method only works here (and for 3/2x½), since above that, there are multiple mixed symmetry terms.
The fact that it contains a 1/3 factor bothers me, since I always find 1/4 with the tableaux, since they are symmetrisation and antisymmetrisation of two terms.
So what is the correct way of transforming a Young tableau into the equivalent tensors?
Last edited: