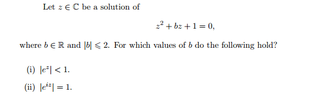Z²+bz+1=0, where |b|≤2. For which values of b do the following hold?

[Stephen Safee]

View attachment 6602
Hello,

This is to check whether my answer is correct or not.
I got for (i) $ $ $0<b\le2$, $ $ and for (ii) $ $ $\pm \frac{1+\pi^2}{\pi}$.

I’m not convinced about the method I used.

I started by finding the two possible roots expressed in terms of $b$, by completing the square.
Now, if (i) is to be true then $z$ must be negative. So, I checked the possible values for $b$ so that $z$ is negative.

For (ii), I used Euler's Identity, and observed that $z=\pmπ$ if (ii) is true. I solved $\pm \pi=-\frac{b}{2}\pm\sqrt{\frac{b^2}{4}-1}$ $ $ to get a value for $b$.

Is this correct? If not, why is this method not giving the correct answer?

Thank you.

 

[HallsofIvy]

Hello,

This is to check whether my answer is correct or not.
I got for (i) $ $ $0<b\le2$, $ $ and for (ii) $ $ $\pm \frac{1+\pi^2}{\pi}$.

I’m not convinced about the method I used.

I started by finding the two possible roots expressed in terms of $b$, by completing the square.
Now, if (i) is to be true then $z$ must be negative. So, I checked the possible values for $b$ so that $z$ is negative.

z must be negative if z is real. Are you assuming that?

For (ii), I used Euler's Identity, and observed that $z=\pmπ$ if (ii) is true.

I suggest you look at Euler's identity again! For $z= \pm\pi$. e^{iz} is 1 and -1. But for z any real number, $|e^{iz}|= 1$.

I solved $\pm \pi=-\frac{b}{2}\pm\sqrt{\frac{b^2}{4}-1}$ $ $ to get a value for $b$.

Is this correct? If not, why is this method not giving the correct answer?

Thank you.

 

[Stephen Safee]

For (i), I deduced that for $z$ to satisfy the equation, it must be real (which doesn't prevent it from also being complex). This is because a non-real complex number cannot be negative. Is this reasoning sound?

EDIT
Following from the above, I have to reconsider my answer for (i).
We have $z=-\frac b2 ± \sqrt{\frac{b^2}{4}-1}$, which means for $z$ to be real, $ $ $b$ can only be $\pm2$.
But if $b=-2$ then $z>0$, which doesn't satisfy (i). $ $ So, in fact, $b=2$.For (ii), I think I get it now. We have

$z=-\frac b2 ± \sqrt{\frac{b^2}{4}-1}$, so

$|e^{i(-\frac b2 ± \sqrt{\frac{b^2}{4}-1})}|=1$

By Euler's formula (as clarified in your post!), we need to find values for $b$ such that $-\frac b2 ± \sqrt{\frac{b^2}{4}-1}\in \mathbb{R}$.

$b=\pm 2$ is the correct answer, because then $\sqrt{\frac{b^2}{4}-1}=0$ and $-\frac b2=\mp1$.

Any other possible value for $b$ is not an option because then $\sqrt{\frac{b^2}{4}-1}$ becomes imaginary. This means multiplying it by the factor $i$ makes it real, which would leave us with $-i\frac b2+x$ (where $x \in \mathbb{R}$) which is $\neq ix$, and so does not satisfy Euler's formula.

---
If the above is still wrong, then please feel free to put me out of my misery with the answer!

 

[I like Serena]

Hi Stephen Safee! Welcome to MHB! (Smile)

Suppose we write $z=x+iy$.

Then for (i):
$$|e^z| = |e^{x+iy}| = |e^{x}|\cdot |e^{iy}| = e^x < 1 \quad\Rightarrow\quad x<0$$
That is:
$$\operatorname{Re}z = -\frac b2 < 0 \quad\Rightarrow\quad b>0$$
We don't care about the imaginary part, which is allowed to be anything.
$z$ can be imaginary as long as the real part is negative.
So your initial result for (i) was correct.

For the record, $z<0$ has no meaning, since the complex numbers cannot be ordered. I'm assuming $\operatorname{Re}z < 0$ is intended.Similarly for (ii):
$$|e^{iz}| = |e^{i(x+iy)}| = |e^{-y + ix}| = e^{-y} = 1 \quad\Rightarrow\quad y=0$$
That is:
$$\operatorname{Im}z = \pm \sqrt{1-\frac{b^2}{4}} = 0 \quad\Rightarrow\quad b=\pm 2$$

 

[Stephen Safee]

Thanks.

There's just one detail that still doesn't make sense to me.

We don't care about the imaginary part, which is allowed to be anything.

But why? It seems I'm just not seeing the logic behind this, which is rather a pain...

So, on one hand we have $z=x+iy$, on the other |e^z|<1, hence |e^(x+iy)|<1. So far, so good.

We cannot say $x+iy<0$. It's indeed absurd, because x+iy is not on the real line to begin with, so it can't either precede or follow any number that is on the real line.

That is, if we could look at all the numbers to the left of 0 we won't see the number x+iy appearing anywhere. Similarly, looking to the right of 0 won't change anything. (This is my understanding of this concept. Is it correct?)

Therefore, x+iy is neither negative nor positive.

How then do we make sense of the inequality $|e^{x+iy}|<1$ ? Well (and clearly here's my mistake), the only way I see is for $iy$ to equal 0, and so for $y$ to equal 0. This assumes that $z$ is real, but you say $z$ can also be complex with an imaginary part. What is then happening to the imaginary part when we write $|e^{x+iy}|=|e^x|<1$ ?

You say nothing, because we don't care about it. My problem is I don't understand what this means in the context described above : (
Obviously, we are not pretending the imaginary part is not there. So what are we doing then?

This is really what is preventing me from understanding what seems to be a rather straightforward concept...

 

[Stephen Safee]

I've got it!

The issue couldn't have been any sillier.

I had forgotten the very specific meaning of the symbol $|$ $ $ $|$ for complex numbers...
Which of course means modulus of the complex number.

Usually, the modulus, when the complex number is written in the cartesian form $x+iy$, is $\sqrt{x^2+y^2}$, so it's simply the distance of the complex number from the origin.

However, when it's written in the exponential form $re^{iy}$, $ $ $r$ is then the modulus.
So, all the question was asking was to rearrange the inequality into the form $|re^{iy}|=r<1$, then deduce the value of $b$ from the value of $r$!

So ultimately, this gives $|e^{x+iy}|=|e^{x}e^{iy}|$, where $r=e^{x}$.
Hence, $|e^{x}e^{iy}|=e^{x}$, by simple definition of the operation $|$ $ $ $|$ for complex numbers.

So, stepping back to the initial inequality, we have $|e^z|=e^x<1$.
Since $x=-b/2$, it follows that to satisfy (i), $b$ can be any number in the interval $(0, 2]$.

PS:
Note to self -- never forget to revise topics you learned months ago before starting to do exercises on them!

 

[MarkFL]

I've got it!...

Thank you for conscientiously coming back to your thread and posting your work to finalize the topic. (Yes)