- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Smile)
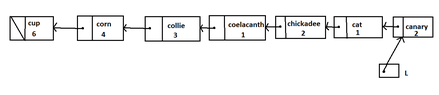
Suppose that each node of a list has the following structs:
It is given a string $w$. Suppose that $w$ is in the list at a node $p$, of which the struct num has the value n.
We are looking for the value of the struct string of the node that precedes $p$ for $n$ positions in the list.View attachment 3606
So, do we have to traverse the whole list, till we find a node with struct num equal to $n$ and then with a while loop find the desired value or is there also a better way? (Thinking)
Suppose that each node of a list has the following structs:
- string
$$$$ - num
$$$$ - next
It is given a string $w$. Suppose that $w$ is in the list at a node $p$, of which the struct num has the value n.
We are looking for the value of the struct string of the node that precedes $p$ for $n$ positions in the list.View attachment 3606
So, do we have to traverse the whole list, till we find a node with struct num equal to $n$ and then with a while loop find the desired value or is there also a better way? (Thinking)