Fundamental question on GR: Basis vector meaning

[teddd]

This is a very basic question in understanding General Relativity, but the answer still eludes me.

The simples way I can state it is: "what exactly represent the 4 basis vector at a certain point on the manifold?"

But let me explain myself.
Let's take a 4 dimensional Minkowsky space.
In this context the 4 basis vectors are of simple interpretation: 3 of them represent the "direction" of the "rulers" an observer use to measure thing and one indicates the time "direction" (ok, this is not 100% correct, but you got the juice). Now any Lorentz transformation mantain the metric in the minkowsky form, and this is ok. I can picture the basis vector of an observer who moves with a certain speed with respect to me and by going in his referment frame I can picture my "old" basis vector: this is a long way to say I have changed basis.
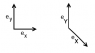
To make this the clearest possible way imagine that a minkowsky space with basis vectors $\vec{e}_t\,,\vec{e}_x\,,\vec{e}_y\,,\vec{e}_z$;and write down the basis vector for an observer who experiment a boost in the x direction.
His basis vector will be $\vec{e}'_t=a\vec{e}_t+b\vec{e}_x$ and $\vec{e}'_x=c\vec{e}_t+d\vec{e}_x$, and $\vec{e}'_y=\vec{e}_y\,,\vec{e}'_z=\vec{e}_z$ and so i can say at which pace his clock goes ecc.
The point is that even in this example the basis vector have a precise meaning.

Now, the question!

"In a curved spacetime what is the meaning of the basis vector at a certain point?"
Do they still indicate the direction of the observer's rulers and the pace of his clock?

Now take any curved manifold.
Here begins the confusion, becaouse when they say that a certain change of basis will put locally the metric in the minkowsky form to me it's like they say that if i want to see the spacetime locally flat I have to set my rulers in a certain direction and set my clock to a certain pace.
Or, put in another way, think of a certain basis vector at a point. Now, change basis to make the metric locally flat. Now you have two basis vector at that point, one corresponding to the first observer (suppose that's me) which doesn't see spacetime flat and another observer (let's call him Adam) whic instead does.

We both are at the same point in spacetime, but Adam moves respect to me with a certain (constant, since we are looking at things in infinitesimal interval) speed, with a certain pace set on his clock.
Now, is this that allow him to see spacetime locally flat? i mean, the only fact that he moves with a certain speed and/or sets his rulers in a particular direction is enough to make the local flatness manifests itself?

This seems strange to me. I don't think it is really like that!
So I am asking myself: does the basis vector at a certain point mean exactly what I have in mind??
Or have I misunderstood the concept of basis transformation? So that they do not mean what I've wrote (this is a restatement of the question above!)

Thanks a lot for the attention fellas!

 

[WannabeNewton]

Here begins the confusion, becaouse when they say that a certain change of basis will put locally the metric in the minkowsky form to me it's like they say that if i want to see the spacetime locally flat I have to set my rulers in a certain direction and set my clock to a certain pace.
Or, put in another way, think of a certain basis vector at a point. Now, change basis to make the metric locally flat.

I lost you here. You aren't making a change of basis to get to the minkowski metric locally. In general, you can't find a coordinate transformation that puts the metric on a curved space in minkowski form. The metric reducing to the minkowski metric locally is a statement of how an open ball in the neighborhood of a point P will be isomorphic to minkowski space - time. Could you explain what you mean?

 

[teddd]

You aren't making a change of basis to get to the minkowski metric locally.

I lost YOU here !

If I'm not mistaking it is a basic concept of GR that a change of basis will reduce the metric to the minkowsky form at first order at a certain point on the manifold, and in that point spacetime IS flat in an infinitesimal neighbour. (It think it's called euqivalence principle, but i could easily be mistaking on the name).

This is a consequence of what you say, that for each point on a smoot manifold there is a tangent plane.

 

[WannabeNewton]

If I'm not mistaking it is a basic concept of GR that a change of basis will reduce the metric to the minkowsky form at first order at a certain point on the manifold, and in that point spacetime IS flat in an infinitesimal neighbour.

Yes, you are right; the important part is that the coordinate system must be found at the point P on the n - manifold. That's why I was confused before because you said a change of basis will make the metric locally flat and I couldn't decide if you were somehow talking about a global transformation or one at P. Thanks for setting me straight =D.

EDIT: Now that I reread that paragraph I see that you had been pretty unambiguous as to what you meant by change of basis. My bad completely. Its like the statement: "change of basis to put the metric in flat form" rings some kind of alarm that blocks the ability to read haha.

 

[WannabeNewton]

Now you have two basis vector at that point, one corresponding to the first observer (suppose that's me) which doesn't see spacetime flat and another observer (let's call him Adam) whic instead does.

Now this I don't get: if they are in the same neighborhood of P then what is stopping both of them from finding coordinate transformations at P such that $g_{\mu \nu } = \eta _{\mu \nu } + O[(x^{\alpha })^{2}]$?

 

[teddd]

Well, all of the vectors you think of in GR lie in the tagent planes to the point they're attached at.
But this doesn't mean that the spacetime will look flat to all observers (always at first order, i may omit this from now on ); you need the first derivatives of the metric to vanish, and that restricts your choice.

I guess that when you have find such a coordinate system performing a Lorentz trasformation will keep the metric locally minkowsky; but I'm not sure so i forward the question to someone who knows it better.


That said, there is nothing stopping nobody: i just want to know if it's only the particular direction of the rulers of Adam and the pace on his clock that allow him to see the spacetime flat (to first order); while I, standing in his exact same point in spacetime but with a different coordinate system and so different basis vectors (BUT always lying in the tangent space at the point), won't.

 

[pervect]

Let's back up a bit. In flat space, we can chose an arbitrary set of basis vectors $\vec{e}_a\,,\vec{e}_b\,,\vec{e}_c\,,\vec{e}_d$, but to make our life easier, what we generally do is chose a set of orthonormal basis vectors.Your notation for $\vec{e}_t\,,\vec{e}_x\,,\vec{e}_y\,,\vec{e}_z$ and your post seems to suggest to me that somehow you are thinking that any set of basis vectors must be orthonormal. This is not the case.

To make life much easier for ourself, we usually introduce a set of basis vectors $\vec{e}_t\,,\vec{e}_x\,,\vec{e}_y\,,\vec{e}_z$ with the properties

$\vec{e}_t\ \, \cdot \, \vec{e}_x = 0, \vec{e}_t\ \, \cdot \, \vec{e}_y=0, \vec{e}_t\ \, \cdot \, \vec{e}_z = 0$
$\vec{e}_x\ \, \cdot \, \vec{e}_y = 0, \vec{e}_x\ \, \cdot \, \vec{e}_z = 0, \vec{e}_y\ \, \cdot \, \vec{e}_z = 0$, i.e. the basis vectors are orthogonal.

In our flat space-time, if we have orthogonal basis vectors, the metric tensor will be diagonal. If we don'[t have orthogonal basis vectors, the metric tensor will not be diagonal. But the space-time will still be flat! It's just that we chose non-orthogonal basis vectors.

The normal part of orthonormal just means that $\vec{e}_t\ \, \cdot \, \vec{e}_t = -1, \vec{e}_x\ \, \cdot \, \vec{e}_x = 1, \vec{e}_y\ \, \cdot \, \vec{e}_y = 1, \vec{e}_z\ \, \cdot \, \vec{e}_z = 1$.

(Note: You might have different sign conventions, in general though you have the dot products being + or - 1, it looked ugly when I wrote it that way though).

With orthonormal basis vectors the metric tensor for our flat space-time is not only diagonal, but the absolute value of the coefficients is unity.

 

[teddd]

You're absolutely right pervect, in fact the flatness/curveness of a manifold cannot be detected with the metric alone, is't requested for the Riemann tensor to vanish.

But you made me think.

Now, i know that i can use whichever basis i want (if I choose it to be orthonormal i will have the minkowsky form); and so, for example, in flat space i can decide to use a polar basis (which is still orthogonal but not orthonormal) or in general any maximal set of linearly independent vector.

So i am pushed to say that in flat space the observer who uses polar basis, and therefore doesn't see the metric as minkowskian, has nothing less to an observer which instead does.
Appliyng this concept on a curved manifold, I'd say that the observer A who sees the space as locally flat (so the metric for him is minkowsky at first order) doesen't have anything more than an observer B which instead has any other kind of metric; it's like A has a particular vierbein which (can I say accidentally?) allow him to see space (infinitesimally) around him flat.
The observer A doesn't have to have particular speed, pace, ecc..; he only has a "lucky" combination of vectors which make the metric flat at first order.

I instead thought that the basis vector that allowed him to see spacetime (locally) flat had a particular physical meaning.
Let me make an explicit example (please!).
Take a 3 dimensional manifold - 1 time dimension and 2 spatial dimesion.
For semplicity take the metric to be $$g_{\mu\nu}=\left(\begin{array}{ccc}-1&0&0\\ 0&\gamma_{ij}&\\ 0&&\end{array} \right)$$so that the timelike basis vector is orthonormal to all spaceike basis vector, which form the purely spatial metric $\gamma_{ij}$ on the spatial hypersurfaces.

Now take the spatial hypersurfaces to be spherical, with unit radius, and choose polar coordinates $(\theta,\phi)$, so that the metric is$$g_{\mu\nu}=\left(\begin{array}{ccc}-1&0&0\\ 0&1&0\\ 0&0&sin^2\theta\end{array} \right)$$Now spacetime is certainly curved, and the observer i choose to write down the metric with doesen't see flat spacetime locally flat except at the point(s) $\mathcal{P}$ on the manifold given by $\mathcal{P}=(t,\theta=0,\phi)$ (here phi is left free, so actually this works all along a curve, but it's only a particular case) where the metric becomes minkowsky and all of the first derivatise vanish (ONLY at $\mathcal{P}$).

Now, does the kinematical/dynamical status of this observer actually mean something physical or is the fact that i can found an observer who sees spacetime locally (as in this case) flat it a mathematical feature that is only used to simplify the calulations?

To complete the example take a point $\mathcal{R}=(t,\hat{\theta}, \phi)$ with a certain fixed theta.
Now, if I change the coordinate system to the new primed set $(t',\theta ',\phi ')$
related to the old by the transformations
$$\begin{array}{ccc} t&= &t'\\ \theta &=&\theta'\\ \phi&= &\frac{\phi'}{sin\hat\theta} \end{array}$$

and i calculate the metric with the basis vectors that these transformation induce i should get

$$g_{\mu\nu}=\left(\begin{array}{ccc}-1&0&0\\ 0&1&\\ 0&0&\frac{sin^2\theta}{sin^2\hat\theta} \end{array} \right)$$

now, at the point $\mathcal{R}$, where $\theta=\hat\theta$ the metric, again, is in the minkowsky form, and its first derivatice vanish as well: the observer who uses these coordinates at $\mathcal{R}$ will see the spacetime as locally flat.

But then again, are some particular physical proprieties that allow him to see the spacetime as flat (at first order)??
Or, instead, the transformation I've made don't implies particular physical meanings but it is only a useful mathematical trick that semplifies my calculations??
I hope I explained myself!

Thanks for the attention!

 

[WannabeNewton]

(Sorry about the other post)
So is your overall question basically: is the equivalence principle the physical reason for why $\partial _{\alpha }g_{\mu \nu } = 0$, to 1st order, in the neighborhood of a point P?

 

[teddd]

My question is: Does the observer who sees the spacetime locally flat in his infinitesimal neighbour have some particular PHYSICAL proprieties that allow him to see spacetime flat
OR
is the fact that I can always find a transformation which makes the metric minkowsky to first order simply a MATHEMATICAL trick that is used only to simplify the calculations?

Thanks for the patience guys!

Really!

 

[WannabeNewton]

What I'm saying is that your ability to find a coordinate transformation such that the metric reduces to the minkowski metric in the neighborhood of that point is, in terms of the physics, a consequence of the equivalence principle. Within that open ball, one cannot differentiate between the gravitational field and acceleration so one cannot identify the tidal forces that are indicative of curvature.

 

[teddd]

You don't seem to be correctly understanding my question!
I think pervect has..

Ps: the manifold I'm considering is DEFINITELY not an open ball!

thanks a lot anyway for your generosity and disponibility, you're great!

 

[WannabeNewton]

I don't think you are understanding me. Pick a point P on the 4 - manifold. The open ball in the neighborhood of P is isomorphic to $\mathbb{R}^{4}$. From this you can say that $\partial _{\alpha }g_{\mu \nu } = 0$ in this neighborhood. The physical analogue of this is that the observer at P cannot tell the difference between the gravitational field and acceleration. Without any way of detecting tidal forces, he says that $\frac{D^{2}\xi ^{\alpha }}{D\tau ^{2}} = 0$ and from this he concludes that $R^{\alpha }_{\beta \mu \nu } = 0$. This is all, of course, to first order and is all a consequence of the equivalence principle.

 

[pervect]

I'm still having a hard time figuring out Tedd's question.

The problem is that "locally flat" seems to mean something specific to Tedd, but I'm not quite sure what it is, it seems to be different from the way I understand it (which is based on MTW's presentation of the term).

Specifically, going to the example:

Now spacetime is certainly curved, and the observer i choose to write down the metric with doesen't see flat spacetime locally flat except at the point(s) P on the manifold given by P=(t,θ=0,ϕ)

What's special about these particular points that makes spacetime "locally flat" there?

The only thing I can see is that the metric is digaonal with the diagonal coefficients being (-1, 1, 1 ) there. Is that what you mean by "locally flat", Tedd?

 

[teddd]

First of all I apologize for my poor explanation!

To wannabeNewton:
ah, i see now what open ball you were referring to!
But still that's not my question. Ok, a locally inertial observer will see geodesics as straight lines but that's not my question!
Maybe i will be more clear in the answet to pervect

To pervect:
with locally flat at a point P I mean that if $g_{\mu\nu}$ is the metric of the observer with some certain basis vector at P you have $$g_{\mu\nu}(P)=\eta_{\mu\nu}\,\,\,,\partial_\alpha g_{\mu\nu}(P)=0\,\,\,,\partial_\beta \partial_\alpha g_{\mu\nu}(P)\neq 0$$
where $\eta_{\mu\nu}$ is the minkowsky metric.

Now in my example in those particular point, with the basis chosen, the metric is locally flat, with the definition of local flatness given above.

if you take instead a generic point on the sphere $P=(t,\hat\theta,\phi)$ to "make" the metric locally flat in that point you have to change basis vectors with the transformation i wrote in the example (which is merely a renormalization).

So the points themselves doesn't have anything in particular, I only choose the basis vector at those points that makes the space looks flat at first order (always with the definition above)




PS: looking back at my example i see now a mistake: when i say that

Now spacetime is certainly curved, and the observer i choose to write down the metric with doesen't see flat spacetime locally flat except at the point(s) P on the manifold given by P=(t,θ=0,ϕ) (here phi is left free, so actually this works all along a curve, but it's only a particular case) where the metric becomes minkowsky and all of the first derivatise vanish (ONLY at P).

I'm actually meaning at the point $\mathcal{P}=(t,\theta=\frac{\pi}{2},\phi)$ !

Distraction misktake...

 

[pervect]

I think your definition of local flatness is what's confusing you. Consider just the first part of your definition.

$$g_{\mu\nu}(P)=\eta_{\mu\nu}$$

By this definition, a perfectly flat plane may or may not meet your requirements for "locally flat" depending on your choice of basis vectors. Which is very awkward at the least. Where did this definition come from?

This goes back to what I was saying earlier, but maybe a diagram will help

Looking at the attached figure, if you chose one particular set of coordinates (x,y) you'll have orthonormal basis vectors ${e}_x$ and ${e}_y$, that is the familiar situation on the left.

You can write formally (I'm not sure if you've seen the notation
$$e_x = \frac{\partial}{\partial x}\,\,e_y = \frac{\partial}{\partial y}$$
given your coordinates x,y, this is called a "coordinate basis" when your basis vectors are the partial derivatives of your coordinates.

I'm not sure if you've been introduced to the notion of basis vectors as partial derivatives, some textbooks take that course of action others don't.

Pictorially, you can see how $e_x$ represents a notion of "an increment in the x direction" and $e_y$ represents "an increment in the y direction", I hope.

I can explain in more depth why we the basis vectors are $\frac{\partial}{\partial x}$ rather than , say, dx, if you need to know, but I don't want to digress from the main point too much, so I'll hold off unless you ask.

Now, how about the diagram on the right? Suppose we make the coordinate substitution:

X = x, Y = x+y

If you have Penrose's "road to reality", you can check out his diagram on pg 190, if not, it's no big deal, it was the inspiration for this.

Then this is a new coordinate system, and the vectors $e_{X}\,\,e_{Y}$ are the coordinate basis for these new coordinates.

One vector represents holding the X coordinate fixed and varying Y, the other vector represents holding the Y coordinate fixed and varying X.

Because the goal of using tensors is to allow arbitrary coordinate systems, it's perfectly valid to have non-unit and/or non-orthogonal basis vectors.

I may have overexplained a bit, actually. Basis vectors do not HAVE to be the coordinate basis vectors, i.e. the partial derivatives, that's just a common choice. You can choose __any__ pair of vectors for your basis vectors on a plane.

Whether or not your metric is diagonal or not has EVERYTHING to do with what choice of basis vectors you made, and NOTHING to do with flatness.

 

[teddd]

Thanks for your attention pervect!

Now, i know the basis of differentia geometry, I'm familiar with the tensor formalism, coordinate basis ecc... but..have you never seen my definition of an observer who sees spacetime locally flat?

I do not mean the spacetime IS flat in that point!

I mean that with a particular basis vector set the metric becomes minkowsky to first order, the connection vanish (only in that point) and to this observer (namely to this basis vector set) geodesics that pass by that point are straight lines (always in an infinitesimal leighbour)


Now, some precisation:
1)
We are not arguing that if I choose a particular basis the spacetime becomes flat.
Flatness-non flatness is an intrinsic propriety of the manifold, and only the riemann tensor (and derivaitves) measure that, and the riemann tensor, being a tensor doesn't depend on the basis you chose, so the global topology of the manifold is untouchable.

2)

By this definition, a perfectly flat plane may or may not meet your requirements for "locally flat" depending on your choice of basis vectors. Which is very awkward at the least. Where did this definition come from?

Yes, to that observer space won't seem locally flat.
But with my definition you can find some basis vector which instead do make the spacetime look locally flat(with the meaning I give in my definition); BUT being in this case the spacetime flat everywhere we have actually built a global inertial frame (which is instead impossible on curved spacetime).



If, as I probably have, did not make myself clear, please point where does the confusion start!
(I'm pretty sure my definiton is correct)

 

[pervect]

Thanks for your attention pervect!

Now, i know the basis of differentia geometry, I'm familiar with the tensor formalism, coordinate basis ecc... but..have you never seen my definition of an observer who sees spacetime locally flat?

Not really - which doesn't mean that someone doesn't do it somewhere. So if you've got a source you want to quote or mention that uses the words this way, feel free to point it out.

However, everything you're saying seems to me to be a statement about the particular coordinate choice you are using.

We could reword what you're saying to "locally flat coordinates" and that would make general sense to me,though the adjective "flat" seems to be not-quite-precise. But the way I see this described usually (MTW, for instance) is "Fermi Normal coordinates". Which have all the properties you describe as long as the observer isn't accelerating. I suppose you could add that to be really specific. So you might say " The fermi normal coordinates of a geodesic observer".

I do not mean the spacetime IS flat in that point!

I mean that with a particular basis vector set the metric becomes minkowsky to first order, the connection vanish (only in that point) and to this observer (namely to this basis vector set) geodesics that pass by that point are straight lines (always in an infinitesimal leighbour)Now, some precisation:
1)
We are not arguing that if I choose a particular basis the spacetime becomes flat.
Flatness-non flatness is an intrinsic propriety of the manifold, and only the riemann tensor (and derivaitves) measure that, and the riemann tensor, being a tensor doesn't depend on the basis you chose, so the global topology of the manifold is untouchable.

That's more or less what I was trying to point out.

2)Yes, to that observer space won't seem locally flat.
But with my definition you can find some basis vector which instead do make the spacetime look locally flat(with the meaning I give in my definition); BUT being in this case the spacetime flat everywhere we have actually built a global inertial frame (which is instead impossible on curved spacetime).If, as I probably have, did not make myself clear, please point where does the confusion start!
(I'm pretty sure my definiton is correct)

What was your question, then? We started out talking about basis vectors, and you seemed to have some questions about their significance.

I think we agree now that in general you can choose your basis vectors any way you want, that you have complete freedom in this regard, but if you want a diagonal metric at some point, you need to choose orthonormal basis vectors at that point.

I don't think it was mentioned this before, but following on, if you want the connection coefficients (the first derivative of the metric) to vanish as well, you need to parallel transport your initial choice of basis vectors. So this condition, combined with the first one, specifies your basis vectors everywhere in the neighborhood.

Furthermore, the worldline of the observer must be a geodesic, and there's only one geodesic through a point, so the initial choice of basis vectors specifies the observer's worldline.

So picking out some point and saying the metric is diagonal there and that the connection coefficeints also vanish is sufficient to describe a unique coordinate system (the coordinate system whose coordinate basis vectors are the ones we've specified), Fermi Normal coordinates.

We haven't addressed the size limitations on this coordinate choice - it may not necessarily cover all of space-time, it will only cover a region of space-time where geodesics through the original point P don't cross.

 

[teddd]

Ok, i think I can restate my question now!

I looked for the source of my definition, it comes from my professor(!); and you're right, i could not find it as i stated in the books I'm currently using (shutz carroll ecc).

I can see that all of the books, as you did, refer to a set of orthonormal basis for which the metric in a certain point on the manifold meets the condition i wrote(metric in that point=minkowsky metric, first derivative of the metric in that point=connection in that point=0; ecc..); so actually is of a set of orthonormal basis we're talking about, or more precisely locally inertial frames. Excuse me for my poor definition!

But actually my question stays the same.
It's true in fact that an observer with an orthonormal basis set in a certain point will see the manifold around him as flat( isn't it?), and that's why it's called locally inertial.
So my question (that kinda answers by itself) were: an observer who sees spacetime around him as (at first order) flat, and thus he has an orhtonormal basis set (or, restating, an oberver in a locally inertial frame), has some phisical difference from the other observers who are not using an orthonormal frame??
Namely, the fact that he points his rulers in a certain direction (as to make them orthonormal) has some physical meaning?
Or this observer is exacly like everyone else at that point, except that the metric to him is more simple and thus the calculation are easier, and so choosing this observer to calculate things is like a mathematical trick?Now, some additional comments on your kind answer:

However, everything you're saying seems to me to be a statement about the particular coordinate choice you are using.

absolutely yes.

I don't think it was mentioned this before, but following on, if you want the connection coefficients (the first derivative of the metric) to vanish as well, you need to parallel transport your initial choice of basis vectors. So this condition, combined with the first one, specifies your basis vectors everywhere in the neighborhood.

This is sure, but only if you impose a torsion free connection (this is only a precisation), since with such a connection length and scalar product are conserverd if you parallel trnasport vectors (in our case basis vector) along the motion on a curve.
If such a frame is called fermi-normal, well, i learned a new thing today!

Furthermore, the worldline of the observer must be a geodesic, and there's only one geodesic through a point, so the initial choice of basis vectors specifies the observer's worldline.

I do not agree with that, you need also to secify the initial 4velocity of the observer, since finding the geodesic through a point is like solving a initial value problem, and you need first derivative (tangent vector) too.
EDITED: ops, i see now that you also asked for the basis to be specified---no problem then, the timelike vector is the four velocity of the observer.

We haven't addressed the size limitations on this coordinate choice - it may not necessarily cover all of space-time, it will only cover a region of space-time where geodesics through the original point P don't cross.

I'm aware of this, but it's not important in this discussion.Really, thanks for your time and attention!PS:Another small question, which i hope won't push the main discussion apart.

...is "Fermi Normal coordinates". Which have all the properties you describe as long as the observer isn't accelerating. I suppose you could add that to be really specific. So you might say " The fermi normal coordinates of a geodesic observer".

why i need him to follow a geodesics (to be a freely falling observer)?
Couldn't I do the same for an observer who is accelerating, and thus follows a generic timelike curve?
If i find a local inertial frame and then i parallel trasnport it along the curve, should't I obtain the same result since the scalar product of the vectors don't vary (always with a metric compatible connection)

 

[Dale]

Furthermore, the worldline of the observer must be a geodesic, and there's only one geodesic through a point, so the initial choice of basis vectors specifies the observer's worldline.

[nitpick]There are an infinite number of geodesics through a point, but a point and a direction from that point (e.g. the timelike basis vector) do specify a unique geodesic.[/nitpick] Sorry to nitpick.

 

[TrickyDicky]

So my question (that kinda answers by itself) were: an observer who sees spacetime around him as (at first order) flat, and thus he has an orhtonormal basis set (or, restating, an oberver in a locally inertial frame), has some phisical difference from the other observers who are not using an orthonormal frame??
Namely, the fact that he points his rulers in a certain direction (as to make them orthonormal) has some physical meaning?
Or this observer is exacly like everyone else at that point, except that the metric to him is more simple and thus the calculation are easier, and so choosing this observer to calculate things is like a mathematical trick?

Well, as you say it answers itself from what you know and have been told here.
There is obviously no physical difference between the observers that depends on the basis sets.
This doesn't mean it doesn't have a physical meaning, as it has been said before the physical name of it is the Equivalence Principle.
There is actually an even deeper geometric cause for this that is not exactly a mathematical trick (but it certainly makes calculations easier), it comes from Riemann and it's in the very definition of manifold, that is the mathematical object with which we model our universe, in this definition you see that any manifold can be considered locally flat.

 

[teddd]

Ok, this has been finally set straight!
Thanks guys!

But to put and end to this post, has anyone an answer to the 2 question aroused from the main discussion?
They were:

1) If I choose, in a certain point, a locally inertial observer and then i perform a Lorentz transformation (in that point), will the resulting observer be locally inertial too (i guess it is)

2) this (sub)question is a little different from the main topic. Anyway here it is.
The metric compatibility condition preserves the geometrical proprieties of parallel transported vector along some curve. Those "geometrical proprieties" include lenght, orthogonality ecc.. .
So if i take an orthomormal set of basis vectors in a certain point Q and i parallel transport them along a certain curve (which doesn't have to be necessairly a geodesic) which extend from Q to a new point R, will the parallel-transported vector be orthonormal at R too?


Thanks!

 

[pervect]

Ok, i think I can restate my question now!


So my question (that kinda answers by itself) were: an observer who sees spacetime around him as (at first order) flat, and thus he has an orhtonormal basis set (or, restating, an oberver in a locally inertial frame), has some phisical difference from the other observers who are not using an orthonormal frame??
Namely, the fact that he points his rulers in a certain direction (as to make them orthonormal) has some physical meaning?
Or this observer is exacly like everyone else at that point, except that the metric to him is more simple and thus the calculation are easier, and so choosing this observer to calculate things is like a mathematical trick?

This starts to get philosophical, but I regard things that are physical as being viewpoint independent, and the choice of basis vectors is a choice of viewpoint.

You'll have to make up your own mind on what constiutes "physical", though, at least as to what criterion something must meet to be called physical.

EDITED: ops, i see now that you also asked for the basis to be specified---no problem then, the timelike vector is the four velocity of the observer.

Exactly

PS:Another small question, which i hope won't push the main discussion apart.

why i need him to follow a geodesics (to be a freely falling observer)?
Couldn't I do the same for an observer who is accelerating, and thus follows a generic timelike curve?

If i find a local inertial frame and then i parallel trasnport it along the curve, should't I obtain the same result since the scalar product of the vectors don't vary (always with a metric compatible connection)

If the observer is accelerating, the covariant derivative of their velocity isn't zero, it's a vector that points in the direction of the acceleration.

If the covariant derivative isn't vanishing, the Christoffel symbols are not either. In fact, you can interpret the Christoffel symbols in a coordinate frame in which you are at rest physically as your absolute acceleration, what you measure with an acceleromter - either a formal instrument, or informally the forces you feel pushing you into your chair.

 

[teddd]

I regard things that are physical as being viewpoint independent, and the choice of basis vectors is a choice of viewpoint.

You'll have to make up your own mind on what constiutes "physical", though, at least as to what criterion something must meet to be called physical.

This is EXACTLY what i tought!

but now, on the 'new' question:

If the observer is accelerating, the covariant derivative of their velocity isn't zero, it's a vector that points in the direction of the acceleration.

Sure. but if i impose that?
I mean, take a curve given whose tangent vector is U, and a basis vector set $e_j$ in a certain point P which forms in that point a locally inertial frame.
Now impose the usual parallel transport condition $\nabla_U\,e_j=0$ for all the basis vectors at the point P.
If the geometrical relationship between the vector is preserved during parallel transport the basis vector should constituite a locally inertial frame all along the curve.

Where's the flaw in that?

again, thanks for the disponibility

 

[pervect]

This is EXACTLY what i tought!

but now, on the 'new' question:


Sure. but if i impose that?
I mean, take a curve given whose tangent vector is U, and a basis vector set $e_j$ in a certain point P which forms in that point a locally inertial frame.
Now impose the usual parallel transport condition $\nabla_U\,e_j=0$ for all the basis vectors at the point P.
If the geometrical relationship between the vector is preserved during parallel transport the basis vector should constituite a locally inertial frame all along the curve.

Where's the flaw in that?

again, thanks for the disponibility

I should clarify my remark - if you have a fermi normal coordinate system, $\Gamma^{x}{}_{tt}$ represents your x-acceleration, $\Gamma^{y}{}_{tt}$ represents your y-accleration, etc. Other connection coefficeints have a different physical interpretation.

As far as transporting a time basis vector along a curve - you can certainly do that, but if you have an accelerating observer, the basis vector you get by this process isn't the same as the time basis vector of the accelerating observer's clock.

Suppose at t=0 your velocity v=0 in some inertial frame I0, and that at time t=1 your velocity has increased to v=a.

If you parallel transport the time basis vector of your initial velocity at t=0 along the curve, you'll be using the time basis vector of the inertial frame I0. It won't match your new basis vectors at t=1 because your velocity has changed.

If we assume you're in the flat space-time of special relativity, if you parallel transport the time basis vector at t=0 along the curve, you'll be using the basis vectors of the global inertial frame I0.

 

[teddd]

As far as transporting a time basis vector along a curve - you can certainly do that, but if you have an accelerating observer, the basis vector you get by this process isn't the same as the time basis vector of the accelerating observer's clock.

Suppose at t=0 your velocity v=0 in some inertial frame I0, and that at time t=1 your velocity has increased to v=a.

If you parallel transport the time basis vector of your initial velocity at t=0 along the curve, you'll be using the time basis vector of the inertial frame I0. It won't match your new basis vectors at t=1 because your velocity has changed.

Basically a locally inertial observer who follows a geodesics will be locally inertial on all of the points on the geodesic (if he parallel transports his basis vectors),
while an acclerating observer won't, (obvioulsy there can be found a locally inertial frame at every point of the curve, but it won't be the very same observer from which we started from).

Another little doubt: the concept of acceleration in general relativity means acceleration with respect to a geodesic (restating: a variation of the path of the geodesic experienced by a particle) represented like you said by those christoffel symbols; it does not mean an absolute acceleration right? becaouse if the partivle has to follow a particular curve it has to vary its velocity from point to point (= its accelerating), if the curve is not straight.

 

[TrickyDicky]

Another little doubt: the concept of acceleration in general relativity means acceleration with respect to a geodesic (restating: a variation of the path of the geodesic experienced by a particle) represented like you said by those christoffel symbols; it does not mean an absolute acceleration right? becaouse if the partivle has to follow a particular curve it has to vary its velocity from point to point (= its accelerating), if the curve is not straight.

Yes, acceleration is relative in this sense, what is perceived as non-acceleration for an observer following its local geodesic is perceived as relative acceleration by a different observer following a different local geodesic, this is the basis of tidal effects and it's taken advantage of in spececraft journeys in the form of gravitational slingshots where local gravitational conditions are used to get a boost and save fuel.
Thus the distinction between proper (absolute) acceleration and coordinate (relative) acceleration.

 

[pervect]

Basically a locally inertial observer who follows a geodesics will be locally inertial on all of the points on the geodesic (if he parallel transports his basis vectors),
while an acclerating observer won't, (obvioulsy there can be found a locally inertial frame at every point of the curve, but it won't be the very same observer from which we started from).

Another little doubt: the concept of acceleration in general relativity means acceleration with respect to a geodesic (restating: a variation of the path of the geodesic experienced by a particle) represented like you said by those christoffel symbols; it does not mean an absolute acceleration right? becaouse if the partivle has to follow a particular curve it has to vary its velocity from point to point (= its accelerating), if the curve is not straight.

You can measure your acceleration via an accelerometer without any reference to another object. In my mind that qualifies acceleration as being "absolute". For instance, velocity is not absolute, because you can only measure the velocity relative to another object.

 

[TrickyDicky]

You can measure your acceleration via an accelerometer without any reference to another object. In my mind that qualifies acceleration as being "absolute".

An accelerometer measures acceleration relative to a free-falling test mass (actually the acceleration of the casing of the accelerometer relative to a damped mass inside the device explained in simple terms).
You are of course free in your mind to consider this as "absolute".

For instance, velocity is not absolute, because you can only measure the velocity relative to another object.

This heuristic fails when you measure the Earth velocity relative to the CMB (doppler dipole).
Unless you consider vacuum as a material object, like aether fans do.

 

[teddd]

Stop!
Before getting deeper in this discussion, could you tell if my conclusion

Basically a locally inertial observer who follows a geodesics will be locally inertial on all of the points on the geodesic (if he parallel transports his basis vectors),
while an acclerating observer won't, (obvioulsy there can be found a locally inertial frame at every point of the curve, but it won't be the very same observer from which we started from).

is correct??

And (i hate to insist, you have to apologize me) does a Lorentz transformation of a locally inertial frame give another locally inertial frame (at the same point?)---I guess it does.


Finally, in my humble opinion, on the acceleration relativeness topic i think TrickyDicky is right!

 

[DrGreg]

Stop!
Before getting deeper in this discussion, could you tell if my conclusion

Basically a locally inertial observer who follows a geodesics will be locally inertial on all of the points on the geodesic (if he parallel transports his basis vectors),
while an acclerating observer won't, (obvioulsy there can be found a locally inertial frame at every point of the curve, but it won't be the very same observer from which we started from).

is correct??

Er, the way you've phrased this, you seem to be asking "will a locally inertial observer ... be locally inertial?". The answer to that is trivially yes. That can't be what you intended to ask, so could you phrase your question more clearly?

 

[teddd]

Well..that may actually be the question!

That's becaouse i used to consider an observer as locally inertial only at one point on manifold: i thought that you have to recalculate directly all of the basis vector if you wanted to get another locally inertial boserver at another point on the curve.

But there is one particular case, namely the one in which the observer follows a geodesics.
In that case the timelike basis vector is parallel transported along the curve, and so if i pick a locally inertial observer on one point of the geodesic (restating: if i choose the basis set that makes the metric minkowsky to first order, that makes all og the chirstoffel symbols vanish ecc..), and i parallel transport this basis vector set i will actually have a locally inertial frame all along the geodesics.

The question arised when i asked pervect why the curve had to be a geodesics, since the condition of parallel transport can be imposed geometrically (post n.24).
He explained to me that i can parallel transport an orthonormal basis vector set on every curve i want and obtain an orthonormal frame everywhere, but if the curve is not a geodesic, by parallel transporting those vectors, I'm actually changing observer: like he said:

As far as transporting a time basis vector along a curve - you can certainly do that, but if you have an accelerating observer, the basis vector you get by this process isn't the same as the time basis vector of the accelerating observer's clock.

Suppose at t=0 your velocity v=0 in some inertial frame I0, and that at time t=1 your velocity has increased to v=a.

If you parallel transport the time basis vector of your initial velocity at t=0 along the curve, you'll be using the time basis vector of the inertial frame I0. It won't match your new basis vectors at t=1 because your velocity has changed.

When instead the locally inertial observer at a certain point on the manifold follows a geodesics (trough that point) the parallel transporting condition (which here is a more physical and less geometrical condition) is coherent with the observer: the time basis vector all along the curve is the time basis vector of the very same observer's clock (so by this process I'm not changing observer).

So we can say that if you pick a locally inertial observer on a certain point A of a geodesic (thus choosing a basis vector set which makes the christoffel symbols vanish at A), that observer will be locally inertial all along the geodesic itself, thus all of the christoffel vanish at every point on the curve (using in those point the basis vectors parallel transported from point A).
I wanted to be sure that what I've written above is right!

 

[pervect]

An accelerometer measures acceleration relative to a free-falling test mass (actually the acceleration of the casing of the accelerometer relative to a damped mass inside the device explained in simple terms).
You are of course free in your mind to consider this as "absolute".


This heuristic fails when you measure the Earth velocity relative to the CMB (doppler dipole).
Unless you consider vacuum as a material object, like aether fans do.

I don't see what you think fails when you measure the Earth's velocity relative to the CMB. It's still a relative measurement. The frame is specified not by the existence of the CMB, but by its isotropy.

But I suspect we're far apart enough in our thinking that there's not a lot of sense talking about it. But I do feel some small obligation to point out there isn't any incosistency between measuring one's speed relative to the CMB and thinking that velocities are relative.

 

[WannabeNewton]

So we can say that if you pick a locally inertial observer on a certain point A of a geodesic (thus choosing a basis vector set which makes the christoffel symbols vanish at A), that observer will be locally inertial all along the geodesic itself, thus all of the christoffel vanish at every point on the curve (using in those point the basis vectors parallel transported from point A).

You are basically saying that a freely falling object will remain in free fall as long as it is not subject to any other forces which is, as DrGreg pointed out, a trivial point.

 

[atyy]

My guess is tedd is asking whether only a geodesic observer can be locally inertial (in the appropriate sense) along his worldline.

Yes, in the sense of Fermi-normal coordinates, as discussed in the paragraph after Eq 9.16 of http://arxiv.org/abs/1102.0529 .