On differentiability on endpoints of an open interval

[jwqwerty]

Before asking a question I would first like to mention the definitions of limit of function and differentiality at x=p

1) Limit of function (f) at x=p
Let E be domain of f and p be a limit point of E. Let Y be the range of f.

If there exists q∈E such that for all ε>0 there exists δ>0 such that for all x∈E for which d(x,p)<δ implies d(f(x),q)<ε. Then we say that f(x)->q as x->p or lim(x->p) f(x)=q

2) Differentiable at x=p (a ≤ x ≤ b)
Let E=[a,b] be domain of f. Let Y be the range of f.

If there exists limit of lim(x->p) s(x) (s(x)=[f(x)-f(p)]/[x-p] , where a< x < b), then f is differentiable at x=p.

Sorry for the long definition! This is my question.

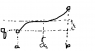
Let E=(a,b) be deomain of f. Let Y be the range of f. Isn't it differentiable at x=a?



As you can see in the picture, we can find a limit 'q' of all ε>0 there exists δ>0 such that for all x∈E for which d(x,p)<δ implies d(f(x),q)<ε. Thus lim(x->a) s(x)=q (by definition 1) )

Please do ask me if anything's unclear!

 

[HallsofIvy]

If we "Let E=(a,b) be domain of f" then f is not even defined at x= a or x= b so certainly not differentiable!

 

[jwqwerty]

If we "Let E=(a,b) be domain of f" then f is not even defined at x= a or x= b so certainly not differentiable!

but look how differentiability at x=p is defined : lim(x->p) s(x)
and this is why i have written definition of limit of function
because there is a close relationship between them

let's look at an example
f(x)=x^2 where domain(E) is E=(0,1) ∪ (1,2) and E⊂R (real number, metric space)
because 1∉E, does this mean lim(x->1) f(x) does not exist?
In fact it does exist, which is 1!

 

[HallsofIvy]

In your first post, you defined s(x)= (f(x)- f(p))/(x- p). If f(p) is not defined, then neither is s(x) for any x.

 

[jwqwerty]

In your first post, you defined s(x)= (f(x)- f(p))/(x- p). If f(p) is not defined, then neither is s(x) for any x.

i still don't get it
by my example, like you said at x=1 it is not defined but there is still a limit value lim(x->1)f(x)
likewise, at x=a it is not defined but there can be a limit value, which is lim(x->a)s(x)

 

[statdad]

Having a limit value at a point does not mean it is defined at that point. Your difference quotient would be
$$\dfrac{f(x) - f(1)}{x-1}$$

If $f(1)$ is not defined, this quotient is not defined.

 

[jwqwerty]

Having a limit value at a point does not mean it is defined at that point. Your difference quotient would be
$$\dfrac{f(x) - f(1)}{x-1}$$

If $f(1)$ is not defined, this quotient is not defined.

E=(0,1) union (1,2)
f is a function from E to R
s is a function from E to R

f(x)=x^2
s(x)=[f(x)-f(1)]/[x-1]

hmm then why is there a difference between existence of limit between these two even though f(x) or s(x) is not defined at x=1?
lim(x->1) f(x)=1 (exists)
lim(x->1) s(x) ? (doesn't exist?)

 

[statdad]

The limit for s does not exist because f(1) is not defined, so there is no number to use in that spot in the numerator.
It is true that your f does not have to be defined at x=1 to have a limit there, because the limit depends only on values of x that are 'close to, but not equal to' 1.
Your fraction doesn't have that property: it requires a value be known for f(1): since f is not defined there it doesn't have a value, so s is not defined.
You can't confuse a limit value with a function value, which is what you're doing.

 

[jwqwerty]

The limit for s does not exist because f(1) is not defined, so there is no number to use in that spot in the numerator.
It is true that your f does not have to be defined at x=1 to have a limit there, because the limit depends only on values of x that are 'close to, but not equal to' 1.
Your fraction doesn't have that property: it requires a value be known for f(1): since f is not defined there it doesn't have a value, so s is not defined.
You can't confuse a limit value with a function value, which is what you're doing.

thanks a bunch :)