- #1
- 1,254
- 141
In an old (2008) thread, DrGreg posted this transformation from a Minkowski chart to a Rindler chart
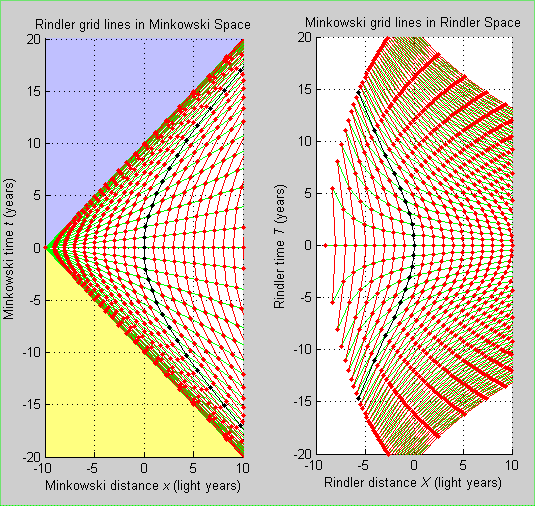
He also wrote:
My question: using these photon worldlines, does a two-way radar measurement give a valid radar distance between two points in the Rindler frame, as per this zoomed view?
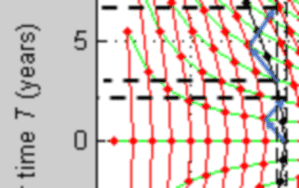
The two vertical dashed lines are Rindler observers and the blue arrows are radar signals send and received by each of them. They attempt to measure the radar distance between the same two inertial particles at different times. If correct, it appears as if the radar distance between the two particles are increasing over time.
-J
PS: I did search for other Rindler threads, but could not find one that quite fits this question. Any links will be welcome.
He also wrote:
I haven't drawn the photon worldlines either, but you can imagine them joining the red dots across the diagonals of each distorted "square" of the grid.
My question: using these photon worldlines, does a two-way radar measurement give a valid radar distance between two points in the Rindler frame, as per this zoomed view?
The two vertical dashed lines are Rindler observers and the blue arrows are radar signals send and received by each of them. They attempt to measure the radar distance between the same two inertial particles at different times. If correct, it appears as if the radar distance between the two particles are increasing over time.
-J
PS: I did search for other Rindler threads, but could not find one that quite fits this question. Any links will be welcome.
