- #1
- 1,647
- 9
In another thread (see [post=2155677]msg #17 of "Only dirty coal can save the Earth"[/post]), user Bystander suggested I lay out more carefully for critical examination the physical basis for the impact of CO2 on climate, so that the assumptions can be seen clearly. This is an excellent idea, and here is my attempt.
This post is a calculation, cited to the literature as forum guidelines advise, quantifying the importance of CO2 to climate. It aims to be transparent, so each step in the calculation is clear and assumptions can be identified.
There's nothing here that is scientifically original or unusual. I am not attempting to cover every factor impacting climate, nor a full account of every period of history. I show that the impact of CO2 is physically bound to be significant in the present. There are other factors, both positive and negative, known and unknown. CO2 is one of the simplest. Its impact is basic physics, and necessarily a major contributor in recent decades.
This thread is not intended to take up every point of climate on which there is disagreement. I am specifically addressing quantification of only one of the many factors involved, to show that CO2 is necessarily significant in the present. I request that we maintain that primary focus, and leave detailed discussion of other aspects of climate science to other threads.
Any point here can be expanded upon as needed. I will defend it vigorously as elementary physics. In my view, and in the view of nearly all scientists working on climate, popular disbelief on this specific point is poorly founded, and supported with bad science. But I will engage disagreement on that with civility and respect, and questions are certainly welcome. I will deal with objections on their own merits, and not by belittling people good enough to come and join in the thread. Be welcome, be comfortable, and for some of you -- be challenged!
The short form
Here's the sequence in summary form.
(1) Energy balance
Earth absorbs about 239 W/m2 from the Sun, accurate to within a couple of percent. This is a global annual average, corresponding to a mean for the whole planet on the time scale of a couple of years, in Watts per square meter.
All of that energy has to go somewhere. Almost all of it is radiated back into space as IR thermal radiation. A small excess can be taken up with Earth's own finite internal stores of energy. The largest available internal store is the heat capacity of the ocean, and recent research indicates that a bit under 1 W/m2 is currently being absorbed into the ocean, as it gradually increases in temperature. This is large by comparison with what is normal for the Earth. The flux into the ocean is known with about 20% accuracy at best; a recent published estimate is 0.85 +/- 0.15 (Hansen et al 2005).
(2) The atmosphere
Earth's atmosphere is the reason why temperatures here are on average so much higher than on our airless moon.
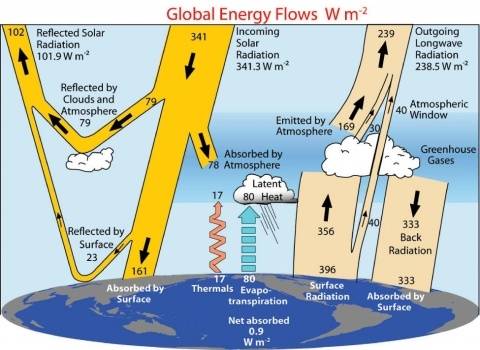
The Earth's surface is radiating something like 390 W/m2 as IR radiation from the surface, known to within a couple of percent. Most of that ends up heating up the atmosphere, which then sheds heat into space. On top of that, thermal convection and heat of evaporation transfers almost another 100 W/m2 into the atmosphere from the surface. Most of the Earth's thermal radiation into space actually comes from the atmosphere.
The atmosphere radiates in all directions, and on average something like 330 W/m2 ends up coming back down to the surface. The net flow of energy is thus something like 60 to 70 W/m2 radiant energy leaving the surface, plus the additional 100 or so W/m2 as convection and latent heat. This is what balances with the energy absorbed at the surface, from the Sun.
Here is a recently published diagram, summarizing how energy flows at present between space, the surface and the atmosphere (Trenberth et al, 2009).
(3) Forcing the energy balance.
Temperature is governed by the flow of energy. The Earth's temperature is at a level that keeps a balance between energy received from the Sun, and emitted back out to space. There can be a small imbalance while excess energy is absorbed or released into the oceans. As equilibrium is reached, the whole planet has average temperatures sufficient for energy balance between solar input and thermal emission back out to space.
If anything occurs to upset the balance, such as a change in the Sun, or in Earth's albedo (reflection), or the atmosphere's composition (absorption), then the temperature of the Earth will respond until the balance is restored. An increase in energy flowing inwards will heat up the surface; and an increase in energy flowing outwards will cool the surface.
A forcing is defined as a change to the energy balance at the top of the troposphere, before balance is restored by changing temperatures. This definition is useful, because the temperature response to different forcings depends mainly on the magnitude of the imbalance, and not so much on how it arises. (Ramaswamy et al 2001)
(4) The forcing of carbon dioxide
Many factors for climate are hard to quantify, but carbon dioxide is one of the most straightforward. The impact, as a forcing, can be calculated. The effect is approximately logarithmic, meaning that the magnitude of the forcing depends on the factor by which concentrations increase. Doubling of concentration is a wildly used benchmark.
The method of calculation is as follows. The atmosphere is treated as a column of gas, with a longwave input at one end (the surface), and short wave input at the other (the Sun). Using the known absorption spectra of gases in the atmosphere, the calculation proceeds line by line through the spectrum to calculate how much radiation is transmitted and absorbed and emitted all along the atmospheric column. The end result is a profile of radiative heating and radiation flux, with a power spectrum of longwave emission at the top, and another for backradiation and solar transmission at the bottom. The calculation is repeated for different gas concentrations, and different conditions. With higher concentrations, the backradiation increases and the emission at the top drops. The forcing, by definition, corresponds to the change in longwave emission at the tropopause.
A standard reference for the calculation is in Myhre et al, (1998). The forcing for any doubling of CO2 is about 3.71 W/m2, or 5.35 per natural log. This is known to high precision for well defined conditions, and to about 10% accuracy in general for the Earth. That is, doubling CO2 in the atmosphere results in 3.7 W/m2 less IR emission escaping into space… until the surface heats up sufficiently to restore the balance.
It is a common convention in the literature to use 2xCO2 as the unit for forcing, rather than W/m2. There are good reasons for this, which are a bit beyond the scope of the post. Essentially, it is because the energy imbalance definition has about five different forms when you really nail it down, whereas doubling of CO2 concentrations is comparatively unambiguous, with a straightforward radiative impact.
(5) The temperature response to forcing -- climate sensitivity
If nothing changes other than temperature, the response is straightforward. Emissions in general are proportional to the fourth power of temperature, and on Earth, with surface temperatures of about 288K and emissions to space of about 240 W/m2, we get about 0.3C for each W/m2 forcing. You can nail that down more carefully, but it does correspond closely to what you get with a radiation transfer calculation. It's called the "Planck response" in climate science. Converting forcing units, this corresponds to about 1.1C per 2xCO2.
In reality, when you change temperature, all kinds of other things start to change as well, someone of which then have an impact of their own on the energy balance. This is called "feedback", and it means the climate response may be amplified, or damped. Several important feedback mechanisms are known (humidity, cloud cover, lapse rate, ice-albedo) and there have been attempts to quantify them. There are both positive and negative feedbacks involved, though the positive feedbacks are stronger. That is, the climate response in reality is rather more than 1.1C per 2xCO2.
For this post, I will use observational constraints. The question is, what is the temperature response in degrees per unit forcing? This is called climate sensitivity, and it can be estimated with data for known episodes of climate change.
One line of research has been study of the brief episode of global cooling that follows a large volcanic eruption. Wigley et al (2005) study a number of eruptions, and three in particular where the data allows estimates of climate sensitivity. The estimates in K/2xCO2 (with 2σ confidence limits) are 2.83{1.28 .. 6.32}, 1.54 {0.3 .. 7.73} and 3.03 {1.79 .. 2.59}. Sensitivity has also been constrained by a number of other cases, most especially the last glacial maximum some 20,000 years ago. There is quite an extensive literature on this, and nearly all of it continues to estimate sensitivity in the range of about 2 to 4.5C. A useful survey and attempt to combine estimates is by Annan and Hargreaves (2006). A very few isolated papers propose lower sensitivities, but these invariably are flawed by plainly identified methodological problems.
(6) The contribution of CO2 to modern warming
We have quite a good idea of atmospheric CO2 levels in recent history. Pre industrial levels are about 280 ppm, and current levels are about 386 ppm. The current rate of increase is about 2ppm/yr.
For any change in CO2 concentrations from A to B, the corresponding change in temperature is going to be S*log2(B/A), where 1.5 < S < 4.5 is the climate sensitivity. You can also use Se*Ln(B/A), where 2.2 < Se < 6.5, which will be easier for most calculators. Best estimate is S=3, or Se = 4.3.
For example, over recent decades the rate of increase of CO2 has been around about 2ppm/year, on top of about 385ppm. The corresponding contribution of CO2 to rising temperature is about Se*Ln(387/385), which is in the range 0.011 to 0.034 C/year, with a best estimate of 0.022 C/year.
Direct measurements indicate that globally averaged surface temperatures on Earth are increasing in recent decades, at around about 0.02 C/year. (Brohan et al, 2005)
There are many factors that must be involved in any credible account of the causes for rising temperatures. It is certainly not driven by CO2 only. The calculations here demonstrate that CO2 is necessarily an important factor, and may help show why it figures so prominently in the scientific literature for modern global climate.
References
In order to keep discussions grounded in legitimate science, the Earth forum requires sources to be peer reviewed. I have therefore given a more than usually thorough list of references for the numbers used in this post.
This post is a calculation, cited to the literature as forum guidelines advise, quantifying the importance of CO2 to climate. It aims to be transparent, so each step in the calculation is clear and assumptions can be identified.
There's nothing here that is scientifically original or unusual. I am not attempting to cover every factor impacting climate, nor a full account of every period of history. I show that the impact of CO2 is physically bound to be significant in the present. There are other factors, both positive and negative, known and unknown. CO2 is one of the simplest. Its impact is basic physics, and necessarily a major contributor in recent decades.
This thread is not intended to take up every point of climate on which there is disagreement. I am specifically addressing quantification of only one of the many factors involved, to show that CO2 is necessarily significant in the present. I request that we maintain that primary focus, and leave detailed discussion of other aspects of climate science to other threads.
Any point here can be expanded upon as needed. I will defend it vigorously as elementary physics. In my view, and in the view of nearly all scientists working on climate, popular disbelief on this specific point is poorly founded, and supported with bad science. But I will engage disagreement on that with civility and respect, and questions are certainly welcome. I will deal with objections on their own merits, and not by belittling people good enough to come and join in the thread. Be welcome, be comfortable, and for some of you -- be challenged!
The short form
Here's the sequence in summary form.
[tex]
\begin{array}{lcll}
\textrm{Energy balance} & \approx 239 & W/m^2 & \textrm{(energy }\text{flux to, and from, space)} \\
\textrm{CO2 forcing} & 3.7 & W/m^2/2xCO_2 & \textrm{(change to balance per doubling)} \\
\textrm{Current CO2 increase} & 2 & ppm/year \\
\textrm{Current 2xCO2 per year} & \log_2(1+2/385) = 0.0075 & 2xCO_2 / year & \textrm{(using 385ppm for current levels)} \\
\textrm{Climate sensitivity} & 3 \pm 1.5 & K/2xCO_2 & \textrm{(Temperature response for forcings, to restore balance)} \\
\textrm{Temperature impact of CO2} & 0.022 \pm 0.011 & K/year & \textrm{Estimated contribution of CO2 to current warming trends}\end{array}
[/tex]
This is a very conventional way of evaluating climate impacts in science. What follows is a brief explanation of the steps, with citations for the numbers and methods.\begin{array}{lcll}
\textrm{Energy balance} & \approx 239 & W/m^2 & \textrm{(energy }\text{flux to, and from, space)} \\
\textrm{CO2 forcing} & 3.7 & W/m^2/2xCO_2 & \textrm{(change to balance per doubling)} \\
\textrm{Current CO2 increase} & 2 & ppm/year \\
\textrm{Current 2xCO2 per year} & \log_2(1+2/385) = 0.0075 & 2xCO_2 / year & \textrm{(using 385ppm for current levels)} \\
\textrm{Climate sensitivity} & 3 \pm 1.5 & K/2xCO_2 & \textrm{(Temperature response for forcings, to restore balance)} \\
\textrm{Temperature impact of CO2} & 0.022 \pm 0.011 & K/year & \textrm{Estimated contribution of CO2 to current warming trends}\end{array}
[/tex]
(1) Energy balance
Earth absorbs about 239 W/m2 from the Sun, accurate to within a couple of percent. This is a global annual average, corresponding to a mean for the whole planet on the time scale of a couple of years, in Watts per square meter.
All of that energy has to go somewhere. Almost all of it is radiated back into space as IR thermal radiation. A small excess can be taken up with Earth's own finite internal stores of energy. The largest available internal store is the heat capacity of the ocean, and recent research indicates that a bit under 1 W/m2 is currently being absorbed into the ocean, as it gradually increases in temperature. This is large by comparison with what is normal for the Earth. The flux into the ocean is known with about 20% accuracy at best; a recent published estimate is 0.85 +/- 0.15 (Hansen et al 2005).
(2) The atmosphere
Earth's atmosphere is the reason why temperatures here are on average so much higher than on our airless moon.
The Earth's surface is radiating something like 390 W/m2 as IR radiation from the surface, known to within a couple of percent. Most of that ends up heating up the atmosphere, which then sheds heat into space. On top of that, thermal convection and heat of evaporation transfers almost another 100 W/m2 into the atmosphere from the surface. Most of the Earth's thermal radiation into space actually comes from the atmosphere.
The atmosphere radiates in all directions, and on average something like 330 W/m2 ends up coming back down to the surface. The net flow of energy is thus something like 60 to 70 W/m2 radiant energy leaving the surface, plus the additional 100 or so W/m2 as convection and latent heat. This is what balances with the energy absorbed at the surface, from the Sun.
Here is a recently published diagram, summarizing how energy flows at present between space, the surface and the atmosphere (Trenberth et al, 2009).
(3) Forcing the energy balance.
Temperature is governed by the flow of energy. The Earth's temperature is at a level that keeps a balance between energy received from the Sun, and emitted back out to space. There can be a small imbalance while excess energy is absorbed or released into the oceans. As equilibrium is reached, the whole planet has average temperatures sufficient for energy balance between solar input and thermal emission back out to space.
If anything occurs to upset the balance, such as a change in the Sun, or in Earth's albedo (reflection), or the atmosphere's composition (absorption), then the temperature of the Earth will respond until the balance is restored. An increase in energy flowing inwards will heat up the surface; and an increase in energy flowing outwards will cool the surface.
A forcing is defined as a change to the energy balance at the top of the troposphere, before balance is restored by changing temperatures. This definition is useful, because the temperature response to different forcings depends mainly on the magnitude of the imbalance, and not so much on how it arises. (Ramaswamy et al 2001)
(4) The forcing of carbon dioxide
Many factors for climate are hard to quantify, but carbon dioxide is one of the most straightforward. The impact, as a forcing, can be calculated. The effect is approximately logarithmic, meaning that the magnitude of the forcing depends on the factor by which concentrations increase. Doubling of concentration is a wildly used benchmark.
The method of calculation is as follows. The atmosphere is treated as a column of gas, with a longwave input at one end (the surface), and short wave input at the other (the Sun). Using the known absorption spectra of gases in the atmosphere, the calculation proceeds line by line through the spectrum to calculate how much radiation is transmitted and absorbed and emitted all along the atmospheric column. The end result is a profile of radiative heating and radiation flux, with a power spectrum of longwave emission at the top, and another for backradiation and solar transmission at the bottom. The calculation is repeated for different gas concentrations, and different conditions. With higher concentrations, the backradiation increases and the emission at the top drops. The forcing, by definition, corresponds to the change in longwave emission at the tropopause.
A standard reference for the calculation is in Myhre et al, (1998). The forcing for any doubling of CO2 is about 3.71 W/m2, or 5.35 per natural log. This is known to high precision for well defined conditions, and to about 10% accuracy in general for the Earth. That is, doubling CO2 in the atmosphere results in 3.7 W/m2 less IR emission escaping into space… until the surface heats up sufficiently to restore the balance.
It is a common convention in the literature to use 2xCO2 as the unit for forcing, rather than W/m2. There are good reasons for this, which are a bit beyond the scope of the post. Essentially, it is because the energy imbalance definition has about five different forms when you really nail it down, whereas doubling of CO2 concentrations is comparatively unambiguous, with a straightforward radiative impact.
(5) The temperature response to forcing -- climate sensitivity
If nothing changes other than temperature, the response is straightforward. Emissions in general are proportional to the fourth power of temperature, and on Earth, with surface temperatures of about 288K and emissions to space of about 240 W/m2, we get about 0.3C for each W/m2 forcing. You can nail that down more carefully, but it does correspond closely to what you get with a radiation transfer calculation. It's called the "Planck response" in climate science. Converting forcing units, this corresponds to about 1.1C per 2xCO2.
In reality, when you change temperature, all kinds of other things start to change as well, someone of which then have an impact of their own on the energy balance. This is called "feedback", and it means the climate response may be amplified, or damped. Several important feedback mechanisms are known (humidity, cloud cover, lapse rate, ice-albedo) and there have been attempts to quantify them. There are both positive and negative feedbacks involved, though the positive feedbacks are stronger. That is, the climate response in reality is rather more than 1.1C per 2xCO2.
For this post, I will use observational constraints. The question is, what is the temperature response in degrees per unit forcing? This is called climate sensitivity, and it can be estimated with data for known episodes of climate change.
One line of research has been study of the brief episode of global cooling that follows a large volcanic eruption. Wigley et al (2005) study a number of eruptions, and three in particular where the data allows estimates of climate sensitivity. The estimates in K/2xCO2 (with 2σ confidence limits) are 2.83{1.28 .. 6.32}, 1.54 {0.3 .. 7.73} and 3.03 {1.79 .. 2.59}. Sensitivity has also been constrained by a number of other cases, most especially the last glacial maximum some 20,000 years ago. There is quite an extensive literature on this, and nearly all of it continues to estimate sensitivity in the range of about 2 to 4.5C. A useful survey and attempt to combine estimates is by Annan and Hargreaves (2006). A very few isolated papers propose lower sensitivities, but these invariably are flawed by plainly identified methodological problems.
Sensitivity is a genuinely open research question with considerable uncertainty. It is, by far, the largest source of uncertainty for the conclusions of this post. I submit that climate sensitivity is very likely in the range 2 to 4.5 K/2xCO2, and highly unlikely to be less than 1.5.
(6) The contribution of CO2 to modern warming
We have quite a good idea of atmospheric CO2 levels in recent history. Pre industrial levels are about 280 ppm, and current levels are about 386 ppm. The current rate of increase is about 2ppm/yr.
For any change in CO2 concentrations from A to B, the corresponding change in temperature is going to be S*log2(B/A), where 1.5 < S < 4.5 is the climate sensitivity. You can also use Se*Ln(B/A), where 2.2 < Se < 6.5, which will be easier for most calculators. Best estimate is S=3, or Se = 4.3.
For example, over recent decades the rate of increase of CO2 has been around about 2ppm/year, on top of about 385ppm. The corresponding contribution of CO2 to rising temperature is about Se*Ln(387/385), which is in the range 0.011 to 0.034 C/year, with a best estimate of 0.022 C/year.
Direct measurements indicate that globally averaged surface temperatures on Earth are increasing in recent decades, at around about 0.02 C/year. (Brohan et al, 2005)
There are many factors that must be involved in any credible account of the causes for rising temperatures. It is certainly not driven by CO2 only. The calculations here demonstrate that CO2 is necessarily an important factor, and may help show why it figures so prominently in the scientific literature for modern global climate.
References
In order to keep discussions grounded in legitimate science, the Earth forum requires sources to be peer reviewed. I have therefore given a more than usually thorough list of references for the numbers used in this post.
- Annan, J. D., and J. C. Hargreaves (2006), http://www.agu.org/pubs/crossref/2006/2005GL025259.shtml, in Geophys. Res. Lett., 33, L06704, doi:10.1029/2005GL025259. (Looks at several observational constraints on sensitivity.)
- P. Brohan, J.J. Kennedy, I. Harris, S.F.B. Tett and P.D. Jones, http://www.agu.org/pubs/crossref/2006/2005JD006548.shtml. J. Geophys. Res., Vol 111, D12106, doi:10.1029/2005JD006548. (Measurement of change to global mean surface temperatures, with the HadCRUT3 dataset.)
- Hansen, J. et. al. (15 authors) (2005) Earth's Energy Imbalance: Confirmation and Implications, in Science, Vol 308, no 5727, pp 1431-1435. (Measurement of a small energy imbalance, and of the net energy flux into the ocean.)
- Myhre et al., (1998) http://www.agu.org/pubs/crossref/1998/98GL01908.shtml, Geophysical Research Letters, Vol 25, No. 14, pp 2715-2718. (Calculation of the CO2 forcing.)
- Ramaswamy, V. et. al. (2001) http://www.grida.no/publications/other/ipcc_tar/?src=/CLIMATE/IPCC_TAR/WG1/212.htm , in Climate Change 2001: The Scientific Basis (Houghton, J. T. et al. eds, Cambridge, U.K.: Cambridge University Press. (Defines radiative forcing.)
- Trenberth, K.E., Fasullo, J.T., and Kiehl, J. (2009) http://ams.allenpress.com/archive/1520-0477/90/3/pdf/i1520-0477-90-3-311.pdf , in Bulletin of the AMS, Vol 90, pp 311-323. (Basic reference for energy flows and energy balance on Earth.)
- Wigley, T. M. L., C. M. Ammann, B. D. Santer, and S. C. B. Raper (2005), Effect of climate sensitivity on the response to volcanic forcing, in J. Geophys. Res., Vol 110, D09107, doi:10.1029/2004JD005557. (Sensitivity estimated from volcanoes.)
Last edited by a moderator: