What is Axiom: Definition and 147 Discussions

An axiom, postulate or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Greek axíōma (ἀξίωμα) 'that which is thought worthy or fit' or 'that which commends itself as evident.'The term has subtle differences in definition when used in the context of different fields of study. As defined in classic philosophy, an axiom is a statement that is so evident or well-established, that it is accepted without controversy or question. As used in modern logic, an axiom is a premise or starting point for reasoning.As used in mathematics, the term axiom is used in two related but distinguishable senses: "logical axioms" and "non-logical axioms". Logical axioms are usually statements that are taken to be true within the system of logic they define and are often shown in symbolic form (e.g., (A and B) implies A), while non-logical axioms (e.g., a + b = b + a) are actually substantive assertions about the elements of the domain of a specific mathematical theory (such as arithmetic).
When used in the latter sense, "axiom", "postulate", and "assumption" may be used interchangeably. In most cases, a non-logical axiom is simply a formal logical expression used in deduction to build a mathematical theory, and might or might not be self-evident in nature (e.g., parallel postulate in Euclidean geometry). To axiomatize a system of knowledge is to show that its claims can be derived from a small, well-understood set of sentences (the axioms), and there may be multiple ways to axiomatize a given mathematical domain.
Any axiom is a statement that serves as a starting point from which other statements are logically derived. Whether it is meaningful (and, if so, what it means) for an axiom to be "true" is a subject of debate in the philosophy of mathematics.

View More On Wikipedia.org
Recent contents Top users
  1. J

    A bizarre riddle using the Axiom of Choice

    I've asked many people about the incredible conclusion of this riddle, whose solution applies the axiom of choice, and have yet to find a satisfying response. I understand the solution, but I would like to know why the axiom of choice leads to such a bizarre result, while being so compatible...
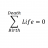
  2. STEMucator

    Show the sup axiom holds for ##\mathbb{Z}##,but not for ##\mathbb{Q}##

    Homework Statement 9. Show that the least upper bound axiom also holds in Z (i.e., each nonempty subset of Z with upper bound in Z has a least upper bound in Z), but that it fails to hold in Q. http://gyazo.com/4c0b79cbb1d15cd5edf0c96ec612a55cHomework Equations I'll split the question into...
  3. M

    Using The Completeness Axiom To Find Supremum and Saximum.

    Homework Statement For each subset of ℝ, give its supremum and its maximum. Justify the answer. {r \in \mathbb{Q} : r2 ≤ 5} Homework Equations Maximum: If an upper bound m for S is a member of S, then m is called the maximum. Supremum: Let S be a nonempty set of ℝ. If S is...
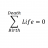
  4. STEMucator

    Proving the Infimum Axiom: Real Analysis Exercise Solution

    Homework Statement So I have started my long journey through N.L. Carothers Real Analysis and my intention is to work through every single exercise along the way. The first problem : http://gyazo.com/ddef0387f04d789c660548c08796585d Homework Equations The Attempt at a Solution...
  5. G

    Can the axiom of countable choice be proved?

    Does anybody know if the axiom of countable choice can be proved? And if it can where I can find a copy of the proof?
  6. B

    Group Axiom Ordering: Proving Associativity First

    Hello, In my abstract algebra class, my teacher really stresses that when you show that a set is a group by satisfying the axioms of a group (law of combination, associativity, identity element, inverse elements) these axioms MUST be proved in order. This makes some amount of sense to me...
  7. N

    Is there a way to prove Axiom of Choice I from Axiom of Choice II?

    I am learning interesting topics in set theory class. I believe that there is a straight proof of Axiom of Choice II by Axiom of Choice I. If you don't know the axioms, see below: Axiom of Choice I states that for any relation R, there is a function F\subseteq R with dom(F) = dom(R)...
  8. B

    The Axiom of Choice: Cardinal Importance in Set Theory

    When I read the AC, "that the ∏ of a coll. of non-∅ sets is itself non-∅" I understand its meaning, yet I come short from understanding its cardinal importance in Axiomatic set theory. I have no exposure "yet" in ZFC but I was hoping if someone could clarify to me why is it that AC is such...
  9. 1

    Is there a named axiom for this?

    "The absolute difference between any two naturals/rationals/reals/complex; is also a natural/rational/real/complex." This should be fairly intuitive but I was wondering if there was a name for this.
  10. M

    What is the difference between assertion and axiom?

    What is the difference between assertion and axiom?
  11. B

    Completeness axiom as having no holes in the set

    Completeness axiom as having "no holes" in the set My textbook describes the completeness axiom as essential to showing that there are no "holes or gaps" in the real numbers. That is, for any two reals A and B, there exists a real C such that A<C<B. Of course, we all know that the actual...
  12. B

    Theorem in applied mathematics that relies on the axiom of choice

    Hi there, Im looking for a theorem that relies on the axiom of choice, but is used in applied mathematics (economics, physics, biology, whatever). In other words a mathematical theory we use to say something about the real world. This is because I'm wondering if discarding the axiom of...
  13. R

    Scalar multiplication axiom, quick question

    u and v are contained in V Lets say the scalar multiplication is defined as: ex. ku=k^2 u or ku = (0,ku2) u=(u1,u2) does this mean that this is also the same for different scalar m? mu=m^2 u or mu = (0,mu2) u=(u1,u2) and does this mean the same for any...
  14. T

    Proving x=y using field axioms in R | Field Axiom Proof

    Homework Statement Using only the fi eld axioms, prove that if x,y ε R and x = y then wx = wy. Homework Equations http://mathworld.wolfram.com/FieldAxioms.html The Attempt at a Solution The solution to this can be solved within 2 lines or so using the field axiom...
  15. J

    Why don't rational numbers fulfill the completeness axiom?

    Homework Statement Show that Q does not fulfill the completeness axiom. Homework Equations "Every non empty set of rational numbers that contains an upper bound contains a least upper bound" (show this is false) The Attempt at a Solution I've sat on this question for a few days...
  16. S

    Axiom of Choice and Metric Spaces.

    So the axiom of choice is confusing to me, apperently there is a distinction between the exsistence of an element and the actual selection of an element? I'm confused as to how much the axiom of choice is needed in elementary metric space theorems? As an example, is the Axiom of Choice needed...
  17. S

    Exploring Axiom of Extension: Naive Set Theory by P.R Halmos

    I am reading Naive set theory by P R Halmos. He says that "The axiom of extension is not just a logically necessary property of equality but a non-trivial statement about belonging." The example for that is "Suppose we consider human beings instead of sets, and change our definition of...
  18. U

    Given g from X onto Y, can we find some f from Y into X without the axiom of choice?

    I thought of this today while eating apples. Suppose we have two arbitrary sets X and Y and a surjection g:X→Y. We seek an injection f:Y→X. Each element of Y has at least one pre-image in X, but there might be more than one; the nonempty sets X_y = \{ x\in X : g(x) = y \} are subsets of X...
  19. C

    Proof of Axiom of Completeness: Bisecting Intervals to Find LUB

    Homework Statement Assume the nested Interval property it true and use a technique similar to the one used to prove the Bolzano Weierstrass theorem, to give a proof of the axiom of completeness. axiom of completeness: Every non-empty set of reals that is bounded above has a least upper bound...
  20. P

    Proof That Product of Two Compact Spaces Is Compact w/o Choice Axiom

    In Theorem 26.7 of Munkres' Topology, it is proved that a product of two compact spaces is compact, and I think the author seems to (rather sneakily) use the choice axiom without mentioning it... Could anyone tell me if this is indeed the case? I don't have a problem with the choice axiom, but...
  21. N

    [topology] new kind of separation axiom? where does it fit in?

    Hello, Just out of curiosity, where would following "seperation axiom" fit in? So far I'm only acquainted with the T1, T2, T3 and T4 axioms (and the notion of completely regular in relation to the Urysohn theorem).
  22. D

    Sets intersection and the axiom of choice?

    I'm working on some topology in \mathbb{R}^n problem, and I run across this: Given \{F_n\} a family of subsets of \mathbb{R}^n , then if x is a point in the clausure of the union of the family, then x \in \overline{\cup F_n} wich means that for every \delta > 0 one has B(x,\delta) \cap...
  23. M

    Proving that the Archimedean axiom is true

    Homework Statement Show that the Archimedean axiom O5 follows from the Least Upper Bound Property O6, together with the other axioms for the reals. Homework Equations O5 = [if a,b > 0, then there is a positive integer n such that b<a+a+a+...+a (n summands)] or [if a,b > 0, then b < na or b/a <...
  24. D

    Countably Infinite Set, Axiom of Choice

    I'm not sure if this question has any sense. Either way, hopefully someone can help me see either the right question or the right way of thinking about this. I don't have any special background in set theory, myself. A set is countably infinite if there is a bijection between it and the...
  25. P

    Relationship between LUB and GLB in Bounded Functions

    Homework Statement h: X x Y --> R is a function from X x Y to R. X,Y nonempty. If range is bounded in R. then let f : X --> R st f(x) = sup{h(x,y): y belongs to Y} (call this set A) g :Y --> R st g(y) = inf{h(x,y) : x belongs to X} (call this set B) Then prove that sup{g(y) : y belongs to...
  26. andrewkirk

    Infinitely recursive sets that don't contradict ZF Axiom of Regularity

    Hello, I have just been reading about the Zermelo-Frankel (ZF) axioms for set theory and thinking about their consequences. I understand that the Axiom of Regularity is needed in order to prevent contradictions like Russell's Paradox arising. That axiom says that any non-empty set A must contain...
  27. A

    Axiom of Choice: finite sets to infinite sets

    So if we have a finite collection of disjoint non-empty sets, one can show using ZF only(with no need of AC) there is a choice function. I understand the reason for this. My confusion is when one goes to non-finite collection of sets. For example if the index set is the Natural numbers, why do...
  28. V

    Explain Axiom of Choice in Simple Terms

    Can someone pretty please explain to me the axiom of choice as unrigorously and casually as possible ;P. And then you could include a rigorous explanation if you wish, but I mean I could just go to wikipedia for that..which I already did... in fact I think I'll include the wiki explanation and...
  29. A

    And the definition of axiom is ?

    And the definition of "axiom" is...? There are (broadly speaking) two basic definitions of the word "axiom". The classical definition, with which Plato, Euclid, and Aristotle wrestled, is roughly this: "An axiom is a proposition for or against which no evidence can be adduced, but the...
  30. R

    Axiom of Schema Foundation

    \exists x \phi(x) \implies \exists x ( \phi(x) \land (\forall y \in x) \lnot \phi(y)), where \; y \; is \; not \; free \; in \; \phi(x) I understand what Russels Paradox is saying and what the difference is between a subset and a member but I'm having trouble with this definition of...
  31. A

    Russell's Paradox and the Axiom Schema of Separation

    As everybody I have read or heard on the matter claims, the Axiom Schema of Separation was concocted to resolve a paradox that results from the Axiom of Unrestricted Comprehension. The Axiom Schema of Unrestricted Comprehension as I understand it is stated as follows (forgive my lack of...
  32. K

    Paradox from Axiom of Choice

    I heard this interesting paradox, which I haven't been able to find anywhere online! Now, bear with me while I set it up! Suppose a professor has a countably infinite number of students. This professor secretly assigns to each student a real number in the interval [0,1], and thus ends up with...
  33. N

    Why the fourth case only with the Axiom of Choice?

    Hello people: IN cardinal domination, a representative set A is dominated by a representative set B iff there's a One-to-One Onto function on A onto a subset of B. This yields four logical cases as the following: Let X dom Y denote "X is dominated by Y". - X dom Y & Y dom X...
  34. Q

    Axiom of Foundation: The Limitations and Implications for Sets in Mathematics

    Why does the axiom of foundation not allow this? a_1 \in a_2 \in a_3 \in a_4 \in a_1 ?
  35. A

    Completeness Axiom Homework: Sets A & B of Positive Rationals

    Homework Statement let A be a set of all positive rational number such that p^2<2 B be a set of all positive rational number such that p^2>2 Homework Equations n/a The Attempt at a Solution Set A is clearly non empty, and is a subset of real number, anyway i can choose 3 is upperbound...
  36. M

    Has the Completeness Axiom Been Disproved?

    Has the completeness Axiom been disproved? see completenessaxiom.com .
  37. K

    Proof of Bolzano-Weierstrass theorem using Axiom of Completeness.

    This is an analysis exercise, I don't get the definition of S. Could anyone explain, please? See the attached pic.
  38. K

    Can detailed balance pricinple(DBP) be derived or is it an axiom?

    In my statistical mechanics class, my prof derived DBP in the following way: Consider a system with many quantum states |a>, |b>..., keep scattering with each other and in equilibrium the master equation give us : \frac{{d{P_k}}}{{dt}} = \sum\limits_{l \ne k} {{T_{kl}}} {P_l} - {T_{lk}}{P_k}...
  39. M

    Whats the difference between a definition and an axiom?

    What is it? For example A function f: A-->B is called injective if, for all a and a' in A, f(a)=f(a') implies that a=a'. What is keeping this definition from being an axiom?
  40. radou

    Topological space satisfying 2nd axiom of countability

    Here's another problem which I'd like to check with you guys. So, let X be a topological space which satisfies the second axiom of countability, i.e. there exist some basis B such that its cardinal number is less or equal to \aleph_{0}. One needs to show that such a space is Lindelöf and...
  41. G

    Noob needs help understanding what is an axiom.

    Wikipedia says this: "In traditional logic, an axiom or postulate is a proposition that is not proved or demonstrated but considered to be either self-evident, or subject to necessary decision. Therefore, its truth is taken for granted, and serves as a starting point for deducing and inferring...
  42. J

    Empty set axiom (proofs in ZF)

    In ZF (or at least the formulation I'm studying), the empty set axiom (\exists \phi)(\forall z)(\neg (z\in \phi)) is a consequence of the other axioms, namely the axiom of infinity (and separation, though googling says that's not necessary) which is (\exists x) (p) where p is some formula to...
  43. J

    Axiom of choice question (small index set)

    Hi there, just wondering what this could mean: "Remark: AC is trivial for |I|=1, since A non-empty means \exists x st x \in A . Similarly for |I| finite (induction on |I|)." I is the index set. As in, our sets are {A_i with i in I}. I'm really not sure what this explanation is getting...
  44. Fredrik

    Zorn's lemma <=> Axiom of choice

    Where can I find the proof of the claim that Zorn's lemma is equivalent to the Axiom of choice?
  45. D

    Vector Space Axiom: Can this be done easier?

    I think, in case it is wrong, I proved the the first vector space axiom for 3 x 3 magic squares; however, there has to be an easier way to do what I did. This pdf has been removed. Go to page 2 of the discussion for an updated version. I attached a pdf file due to I can create the...
  46. D

    Axiom 6 Vector Space: Proving ℝ+ is a Vector Space

    {∀ x ϵ ℝ+ : x>0} Define the operation of scalar multiplication, denoted ∘, by α∘x = x^α, x ϵ ℝ+ and α ϵ ℝ. Define the operation of addition, denoted ⊕, by x ⊕ y = x·y, x, y ϵ ℝ+. Thus, for this system, the scalar product of -3 times 1/2 is given by: -3∘1/2 = (1/2)^-3 = 8 and the sum of 2 and...
  47. D

    Simple Geometry Proof (Betweenness Axiom)

    Homework Statement Given a line l, a point A on l, and a point B not on l. Then every point of the ray AB (except A) lies on the same side of l as B. Homework Equations The Attempt at a Solution I understand why this is true, however I'm having some trouble wording my proof...
  48. K

    What is the difference between adherent points and accumulation/limit points?

    1) "Least upper bound axiom: Every non-empty set of real numbers that has an upper bound, has a least upper bound." Why does it have to be non-empty? Is there an upper bound for the empty set? 2) "It can be proved by induction that: every natural number "a" is of the form 2b or 2b+1 for...
  49. G

    Axiom , Postulate , or Premise ?

    "Axiom", "Postulate", or "Premise"? "Axiom," "postulate," and "premise" have similar meanings, and I often see them used interchangeably, but is there a rule for when to use each one?
  50. E

    Axiom of Choice to prove two propositions

    Hi everyone, we recently covered some implications of the AC and are now to prove the followings statements with the help of the AC or one of its equivalent: (1) Every uncountable set has a subset of cardinality \aleph_1 (the least initial ordinal not less or equal than \aleph_0, the latter...
Back
Top